
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间.
的单调区间.
(Ⅱ)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() ,
,![]()
![]() 恰为
恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
【答案】(I)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)求出函数![]() 的导数,讨论
的导数,讨论![]() 的取值,利用导数判断函数
的取值,利用导数判断函数![]() 的单调性与单调区间;(II)对函数
的单调性与单调区间;(II)对函数![]() 求导数,利用极值的定义得出
求导数,利用极值的定义得出![]() 时存在两正根
时存在两正根![]() 、
、![]() ;再利用判别式以及根与系数的关系,结合零点的定义,构造函数,利用导数即可求出函数
;再利用判别式以及根与系数的关系,结合零点的定义,构造函数,利用导数即可求出函数![]() 的最小值.
的最小值.
试题解析:(Ⅰ)![]() 函数
函数![]() ,
,![]() ,
,![]() ;
;
当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
![]() 当
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ; ...(5分)
; ...(5分)
(Ⅱ)![]() ,则
,则![]() ,
,
![]() 的两根
的两根![]() 、
、![]() 即为方程
即为方程![]() 的两根;
的两根;
又![]() ,
,
![]() ,
,![]() ,
,![]() ; ...(7分)
; ...(7分)
又![]() ,
,![]() 为
为![]() 的零点,
的零点,
![]() ,
,![]()
两式相减得![]() ,
,
得 ,
,
而![]() ,
,


 , ...(10分)
, ...(10分)
令![]() ,
,
由![]() 得
得![]() ,
,
因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,
,
![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,
,![]() ; ...(12分)
; ...(12分)
设![]() ,
,
![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
![]() .
.
即![]() 的最小值为
的最小值为![]() ...(14分)
...(14分)


科目:高中数学 来源: 题型:
【题目】据悉遵义市红花岗区、汇川区2017年现有人口总数为110万人,如果年自然增长率为![]() %,试解答以下问题:
%,试解答以下问题:
(1)写出经过![]() 年后,遵义市人口总数
年后,遵义市人口总数![]() (单位:万人)关于
(单位:万人)关于![]() 的函数关系式;
的函数关系式;
(2)计算10年以后遵义市人口总数(精确到0.1万人);
(3)计算经过多少年后遵义市人口将达到150万人(精确到1年)
(参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有红、白两种颜色的小球共7个,它们除颜色外完全相同,从中任取2个,都是白色小球的概率为![]() ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
(1)求![]() ;
;
(2)求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
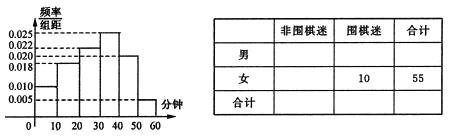
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为D,若函数
的定义域为D,若函数![]() 满足条件:存在
满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”,若函数
为“倍缩函数”,若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,其左、右顶点为
,其左、右顶点为![]() 、
、![]() ,椭圆与
,椭圆与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,![]() 的外接圆的圆心
的外接圆的圆心![]() 在直线
在直线![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)已知直线![]() :
:![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() ,垂足为
,垂足为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: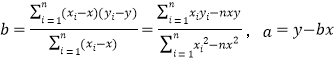 ,).
,).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com