
(08年长沙一中一模文)如图,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
![]() 。
。
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。

解析: 解法一:(1)因为![]() 平面ABC,
平面ABC,![]() 平面
平面![]() ,所以
,所以![]() (2分)
(2分)
![]() 中,
中,![]() ,且
,且![]() 为
为![]() 中点,所以
中点,所以![]() 。
。
又![]() ,所以
,所以![]() 平面
平面![]() (4分)
(4分)
(2)如图,
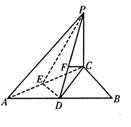
取![]() 中点E,连结
中点E,连结![]() 、
、![]() ,则
,则![]() ,
,
所以![]() (或其补角)为异面直线
(或其补角)为异面直线![]() 与
与![]() 所成的角。(5分)
所成的角。(5分)
因为![]() ,所以
,所以![]() ;
;
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() (6分)
(6分)
在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
在![]() 中,因为
中,因为![]() ,
,
所以![]() 。
。
在![]() 中,因为
中,因为![]() 。所以
。所以![]() 。
。
即异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() 。(8分)
。(8分)
(3)如图,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 。
。
因为![]() ,
,
所以![]() 平面
平面![]() (10分)
(10分)
在![]() 中,
中,![]() 。
。
所以点![]() 到平面
到平面![]() 的距离是
的距离是![]() 。
。
解法二:如图,以C为原点,分别以直线![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系。(1分)
轴建立空间直角坐标系。(1分)
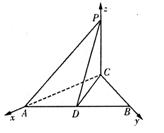
则![]()
所以![]() 中点
中点![]()
(1)因为![]() (2分)
(2分)
所以![]()
![]()
所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() 。(4分)
。(4分)
(2)![]() (6分)
(6分)
所以![]()
即异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() (8分)
(8分)
(3)设平面![]() 的法向量
的法向量![]() ,因为
,因为![]()
则由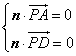 , 得
, 得![]()
取![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量(10分)
的一个法向量(10分)
又![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离![]() (12分)
(12分)
解法三:(1)、(2)同解法一。
(3)设点C到平面PAD的距离为![]() ,
,
由(1)![]() 平面
平面![]() ,
,
因为![]() ,由三垂线定理,可得
,由三垂线定理,可得![]() ,
,
又![]() ,
,
所以![]() ,
,
![]() 。(10分)
。(10分)
由![]() ,得
,得![]()
即![]() ,
,
解得![]()
所以点C到平面![]() 的距离是
的距离是![]() (12分)
(12分)


科目:高中数学 来源: 题型:
(08年长沙一中一模文)某班教室共5组,每组坐6人,4男2女,现王老师对每组采用简单随机抽样的方法抽查作业,规定:每组抽3人,抽到2名男生1名女生为最佳抽查。
(1)若甲坐第一组,乙坐第二组,丙坐第三组,求他们中恰有两人被抽查的要概率;
(2)求第一组为最佳抽查的概率;
(3)全班5组恰有3组为最佳抽查的概率。查看答案和解析>>
科目:高中数学 来源: 题型:
(08年长沙一中一模文)如图,已知![]() 、
、![]() 为平面上的两个定点,
为平面上的两个定点,![]() 为动点,
为动点,
![]() 且
且![]() (
(![]() 是
是![]() 和
和![]() 的交点)。
的交点)。
(1)建立适当的平面直角坐标系求出点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹上存在两个不同的点A、B,且线段AB的中垂线与
的轨迹上存在两个不同的点A、B,且线段AB的中垂线与![]() (或
(或![]() 的延长线)相交于一点
的延长线)相交于一点![]() ,证明:
,证明:![]() (
(![]() 为
为![]() 的中点)。
的中点)。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com