练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过点作抛物线的两条切线,切点分别为,,,分别交轴于,两点,为坐标原点,则与的面积之比为( )

    A. B. C. D.

    【答案】C

    【解析】

    求出切线方程，得出A，B两点坐标，计算E，F坐标，再计算三角形面积得出结论．

    设过P点的直线方程为：y=k（x﹣2）﹣1，代入x2=4y可得x2﹣4kx+8k+4=0，①

    令△=0可得16k2﹣4（8k+4）=0，解得k=1．

    ∴PA，PB的方程分别为y=（1+）（x﹣2）﹣1，y=（1﹣）（x﹣2）﹣1，

    分别令y=0可得E（，0），F（1﹣，0），即|EF|=2．

    ∴S△PEF=

    解方程①可得x=2k，

    ∴A（2+2，3+2），B（2﹣2，3﹣2），

    ∴直线AB方程为y=x+1，|AB|=8，

    原点O到直线AB的距离d=，

    ∴S△OAB=，

    ∴△PEF与△OAB的面积之比为．

    故答案为：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某超市为顾客提供四种结账方式：现金、支付宝、微信、银联卡.若顾客甲没有银联卡，顾客乙只带了现金，顾客丙、丁用哪种方式结账都可以，这四名顾客购物后，恰好用了其中的三种结账方式，那么他们结账方式的可能情况有（ ）种

    A. 19B. 7C. 26D. 12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为 (为参数)。在以坐标原点为极点，轴正半轴为极轴的极坐标系中，曲线。

    （1）写出曲线，的普通方程；

    （2）过曲线的左焦点且倾斜角为的直线交曲线于两点，求。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区上年度电价为元/（），年用电量为．本年度该地政府实行惠民政策，要求电力部门让利给用户，将电价下调到元/（）至元/（）之间，而用户的期望电价为元/（）．经测算，下调电价后新增用电量和实际电价与用户的期望电价的差成反比（比例系数为）．该地区的电力成本价为元/（）．

    （1）写出本年度电价下调后电力部门的收益（单位：元）关于实际电价（单位：元/（）的函数解析式；（收益实际用电量（实际电价成本价））

    （2）设，当电价最低定为多少时，可保证电力部门的收益比上年至多减少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，且直线经过曲线的左焦点．

    （1）求的值及直线的普通方程；

    （2）设曲线的内接矩形的周长为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》（国发[2016〕74号）的要求，到2020年，全国化学需氧量排放总量要控制在2001万吨以内，要比2015年下降10%假设“十三五”期间每一年化学需氧量排放总量下降的百分比都相等，2015年后第年的化学需氧量排放总量最大值为万吨.

    （1）求的解析式；

    （2）求2019年全国化学需氧量排放总量要控制在多少万吨以内（精确到1万吨）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于的方程的解集中只含有一个元素，则的取值集合为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的的参数方程为（其中为参数），以坐标原点为极点，轴的正半轴为极轴的极坐标系中，点的极坐标为，直线经过点．曲线的极坐标方程为.

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）过点作直线的垂线交曲线于两点(在轴上方)，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个工厂在某年连续10个月每月产品的总成本y（万元）与该月产量x（万件）之间有如下一组数据：

    x

    1.08

    1.12

    1.19

    1.28

    1.36

    1.48

    1.59

    1.68

    1.80

    1.87

    y

    2.25

    2.37

    2.40

    2.55

    2.64

    2.75

    2.92

    3.03

    3.14

    3.26

    （1）通过画散点图，发现可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

    （2）①建立月总成本y与月产量x之间的回归方程；

    ②通过建立的y关于x的回归方程，估计某月产量为1.98万件时，此时产品的总成本为多少万元？

    （均精确到0.001）

    附注：①参考数据：，

    ，

    ②参考公式：相关系数，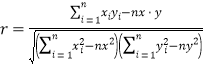

    回归方程中斜率和截距的最小二乘估计公式分别为：．

    查看答案和解析>>

    同步练习册答案