[题目]如图所示的空间几何体中.四边形是边长为2的正方形. 平面. . . . .(1)求证:平面平面,(2)求平面与平面所成的锐二面角的余弦值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图所示的空间几何体中，四边形是边长为2的正方形，平面，，，， .

（1）求证：平面平面；

（2）求平面与平面所成的锐二面角的余弦值.

【答案】（1）见解析；（2）

【解析】试题分析：（Ⅰ）欲证明平面平面，可通过证明平面，需证明，，结合 , 进行证明；
（Ⅱ）构造平面与平面所成二面角的平面角，则，，即可求得答案；

试题解析：（1）证明：连接交于点，则

设的中点分别为，连接，则，

连接，则且，所以，所以

由于平面，所以

所以，，所以平面

所以平面平面

（2）∵，∴

∴平面与平面所成的锐二面角即为平面与平面所成的锐二面角

连接，∵平面，，∴

∴为平面与平面所成二面角的一个平面角

∵，，∴

∴

即平面与平面所成的锐二面角的余弦值为

练习册系列答案

金榜题名系列丛书新课标快乐假期寒系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知圆，圆心为，定点，为圆上一点，线段上一点满足，直线上一点，满足．

（Ⅰ）求点的轨迹的方程；

（Ⅱ）为坐标原点，是以为直径的圆，直线与相切，并与轨迹交于不同的两点．当且满足时，求面积的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

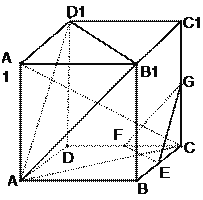
【题目】如图，在棱长为ɑ的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．

（1）求直线C与平面ABCD所成角的正弦的值；

（2）求证：平面A B1D1∥平面EFG；

（3）求证：平面AA1C⊥面EFG ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
（Ⅰ）求直方图中a的值；
（Ⅱ）若将频率视为概率，从该城市居民中随机抽取3人，记这3人中月均用水量不低于3吨的人数为X，求X的分布列与数学期望．
（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值（精确到0.01），并说明理由．