|
|
|
已知函数 y=cosx与y=sin(2x+φ)(0≤φ≤0),它们的图象有一个横坐标为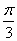 的交点,则φ的值是________. 的交点,则φ的值是________.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:苏教版(新课标) 必修1
题型:
|
|
|
设函数f(x)的定义域为R,若存在常数M>0,使|f(x)|≤M|x|对一切实数x均成立,则称f(x)为“倍约束函数”.现给出下列函数:①f(x)=2x;②f(x)=x2+1;
③f(x)=sinx+cosx;④f(x)=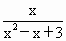 ;⑤f(x)是定义在实数集R上的奇函数,且对一切x1,x2均有|f(x1)-f(x2)|≤ ;⑤f(x)是定义在实数集R上的奇函数,且对一切x1,x2均有|f(x1)-f(x2)|≤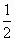 |x1+x2|.其中是“倍约束函数”的有________. |x1+x2|.其中是“倍约束函数”的有________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.
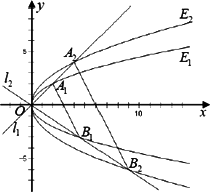
(1)证明:A1B1∥A2B2;
(2)过原点O作直线(异于l1,l2)与E1,E2分别交于C1,C2两点.记?A1B1C1与的△A2B2C2面积分别为S1与S2,求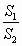 的值. 的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设x,y满足约束条件 ,则z=x+4y的最大值为________. ,则z=x+4y的最大值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且 . .
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程. 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数 f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,在平面直角坐标系 xOy中,F1、F2分别是椭圆 的左、右焦点,顶点B的坐标为(0,b),连结BF2交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连结F1C. 的左、右焦点,顶点B的坐标为(0,b),连结BF2交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连结F1C.
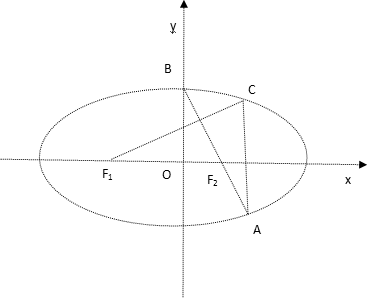
(1) 若点C的坐标为(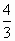 , , ),且BF2= ),且BF2=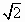 ,求椭圆的方程; ,求椭圆的方程;
(2) 若F1C⊥AB,求椭圆离心率e的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
平面上以机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等.若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是________.
|
|
|
查看答案和解析>>
