练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设点是抛物线上的动点，是的准线上的动点，直线过且与（为坐标原点）垂直，则点到的距离的最小值的取值范围是（ ）

    A. B. C. D.

    【答案】B

    【解析】

    设出点坐标，表示出直线，将点到直线的距离转化成，与直线平行且与抛物线相切的直线与直线间的距离.再找到其取值范围.

    抛物线的准线方程是

    若点的坐标为，此时直线的方程为，

    显然点到直线的距离的最小值是1

    若点的坐标为，其中

    则直线的斜率为

    直线的斜率为

    直线的方程为

    即，

    设与直线平行且与抛物线相切的直线方程为

    代入抛物线方程得

    所以

    解得

    所以与直线平行且与抛物线相切的直线方程为

    所以点到直线的距离的最小值为直线与直线的距离，即

    因为

    所以

    综合两种情况可知点到直线的距离的最小值的取值范围是

    所以选B项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}满足a1+a4＝18，a2+a5＝36．

    （1）求数列{an}的通项公式an；

    （2）若数列{bn}满足bn＝an+log2an，求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过300）：

    空气质量指数

    空气质量等级

    1级优

    2级良

    3级轻度污染

    4级中度污染

    5级重度污染

    6级严重污染

    该社团将该校区在2018年11月中10天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率.

    （Ⅰ）以这10天的空气质量指数监测数据作为估计2018年11月的空气质量情况，则2018年11月中有多少天的空气质量达到优良？

    （Ⅱ）已知空气质量等级为1级时不需要净化空气，空气质量等级为2级时每天需净化空气的费用为1000元，空气质量等量等级为3级时每天需净化空气的费用为2000元.若从这10天样本中空气质量为1级、2级、3级的天数中任意抽取两天，求这两天的净化空气总费用为3000元的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费用支出(百万)与销售额(百万)之间有如下的对应数据:


    2

    4

    5

    6

    8


    30

    40

    60

    50

    70

    (1)画出散点图;

    (2)求回归直线方程;

    (3)据此估计广告费用为10(百万)时,销售收入的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】地球海洋面积远远大于陆地面积，随着社会的发展，科技的进步，人类发现海洋不仅拥有巨大的经济利益，还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日，某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试，并按测试成绩(单位：分)分组如下：第一组，第二组，第二组，第四组，第五组，得到频率分布直方图如下图：

    (1)求实数的值；

    (2)若从第二组、第五组的学生中按组用分层抽样的方法抽取9名学生组成中国海洋实地考察小队，出发前，用简单随机抽样方法从9人中抽取2人作为正、副队长，求“抽取的2人为不同组”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝ex（x﹣a）2+4．

    （1）若f（x）在（﹣∞，+∞）上单调递增，求a的取值范围；

    （2）若x≥0，不等式f（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，我国某海岸线可看作由圆弧AB和射线BC连接而成，其中圆弧AB所在圆O的半径为12海里，圆心角为120°，规定外轮除特许外，不得进入离我国海岸线12海里以内的区域．在港口A处设有观察站，外轮一旦进入规定区域，观察站会接收到预警信号，现从A处测得一外轮在北偏东60°，距离港口x海里的P处，沿直线PA方向航行．

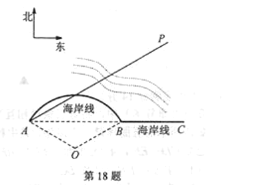
    （1）当x＝30时，分别求出外轮到海岸线BC和弧AB的最短距离，并判断观察站是否接收到预警信号？

    （2）当x为何值时，观察站开始接收到预警信号？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a、b、c为△ABC的三个内角A、B、C的对边，向量=（-1，），=（cosA，sinA），若⊥，且acosB+bcosA=csinC，则角B的大小为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右两个焦点分别为，P是椭圆上位于第一象限内的点，轴，垂足为Q，，，的面积为.

    （1）求椭圆F的方程：

    （2）若M是椭圆上的动点，求的最大值，并求出取得最大值时M的坐标.

    查看答案和解析>>

    同步练习册答案