
已知函数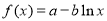 (
(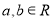 ),其图像在
),其图像在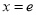 处的切线方程为
处的切线方程为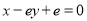 .函数
.函数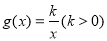 ,
, .
.
(1)求实数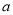 、
、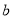 的值;
的值;
(2)以函数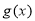 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆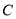 ,若圆
,若圆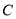 上存在两个不同的点到原点
上存在两个不同的点到原点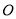 的距离为1,求
的距离为1,求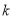 的取值范围;
的取值范围;
(3)求最大的正整数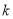 ,对于任意的
,对于任意的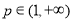 ,存在实数
,存在实数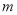 、
、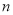 满足
满足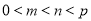 ,使得
,使得 .
.
(1)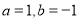 ;(2)
;(2)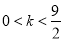 ;(3)
;(3)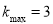 .
.
【解析】
试题分析:(1)由已知可先求出切点坐标和斜率,又切点在函数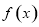 图象上,且在该处的导数等于切线的斜率,从而可列方程组为
图象上,且在该处的导数等于切线的斜率,从而可列方程组为 ,故可求出实数
,故可求出实数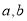 的值;(2)根据题意可将问题转化为圆
的值;(2)根据题意可将问题转化为圆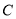 与以原点
与以原点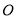 为圆心、1为半径的圆
为圆心、1为半径的圆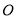 有两个不同交点,即两圆相交,考虑到两圆的半径差为1、和为3,所以两圆心距离的范围应为
有两个不同交点,即两圆相交,考虑到两圆的半径差为1、和为3,所以两圆心距离的范围应为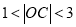 ,再通过配方法,从而可求出实数
,再通过配方法,从而可求出实数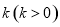 的取值范围;(3)考虑到函数
的取值范围;(3)考虑到函数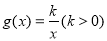 在区间
在区间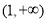 上为减函数,又
上为减函数,又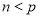 ,所以
,所以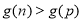 ,若
,若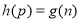 ,则对任意
,则对任意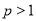 ,有
,有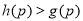 ,即当
,即当 时,要有
时,要有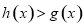 ,整理有
,整理有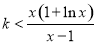 ,令
,令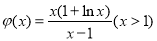 ,由函数的单调性、最值及零点可得
,由函数的单调性、最值及零点可得 ,从而问题可得证,这题有一定难度.
,从而问题可得证,这题有一定难度.
试题解析:(1) 当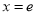 时,
时, ,
,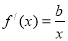 ,故
,故 ,解得
,解得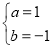 . 3分
. 3分
(2)问题即为圆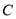 与以
与以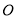 为圆心1为半径的圆有两个交点,即两圆相交.设
为圆心1为半径的圆有两个交点,即两圆相交.设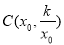 ,则
,则 ,即
,即 ,
,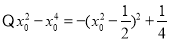 ,
,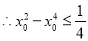 ,
,
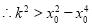 必定有解; 6分
必定有解; 6分
 ,
,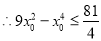 ,
,
故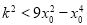 有解,须
有解,须 ,又
,又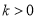 ,从而
,从而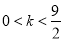 . 8分
. 8分
(3)显然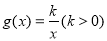 在区间
在区间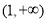 上为减函数,于是
上为减函数,于是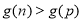 ,若
,若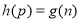 ,则对任意
,则对任意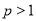 ,有
,有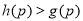 .
.
当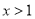 时,
时,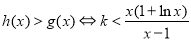 ,令
,令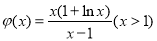 ,
,
则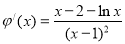 .令
.令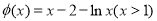 ,则
,则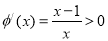 ,故
,故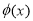 在
在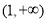 上为增函数,又
上为增函数,又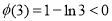 ,
,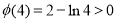 ,因此存在唯一正实数
,因此存在唯一正实数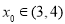 ,使
,使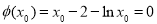 .故当
.故当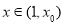 时,
时,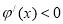 ,
,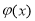 为减函数;当
为减函数;当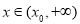 时,
时,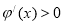 ,
,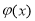 为增函数,因此
为增函数,因此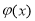 在
在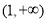 有最小值
有最小值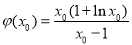 ,又
,又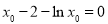 ,化简得
,化简得 ,
,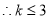 . 13分
. 13分
下面证明:当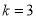 时,对
时,对 ,有
,有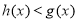 .
.
当 时,
时,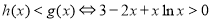 .令
.令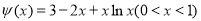 ,
,
则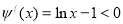 ,故
,故 在
在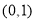 上为减函数,于是
上为减函数,于是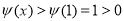 .
.
同时,当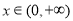 时,
时,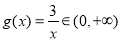 .
.
当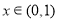 时,
时,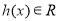 ;当
;当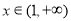 时,
时,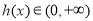 .
.
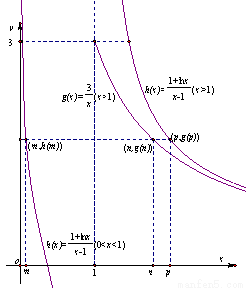
结合函数的图像可知,对任意的正数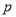 ,存在实数
,存在实数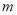 、
、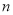 满足
满足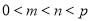 ,使得
,使得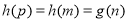 .
.
综上所述,正整数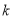 的最大值为3. 16分
的最大值为3. 16分
考点:1.函数单调性、最值;2.导数;3.圆的位置关系.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:解答题
已知函数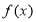 ,当
,当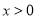 时,
时, .
.
(1)若函数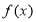 在区间
在区间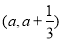
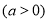 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围;
(2)如果当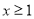 时,不等式
时,不等式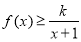 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)试证明: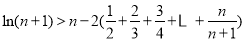
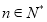 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
以下命题中:①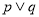 为假命题,则
为假命题,则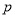 与
与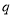 均为假命题
均为假命题
②对具有线性相关的变量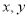 有一组观测数据
有一组观测数据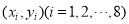 ,其回归直线方程是
,其回归直线方程是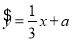 ,且
,且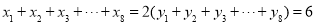 ,则实数
,则实数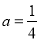
③对于分类变量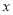 与
与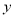 它们的随机变量
它们的随机变量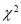 的观测值
的观测值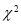 来说
来说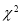 越小.“
越小.“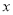 与
与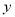 有关联”的把握程度越大
有关联”的把握程度越大
④已知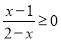 ,则函数
,则函数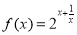 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:解答题
如图,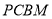 是直角梯形,∠
是直角梯形,∠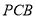 =90°,
=90°,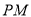 ∥
∥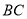 ,
,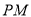 =1,
=1,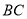 =2,又
=2,又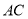 =1,∠
=1,∠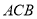 =120°,
=120°,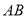 ⊥
⊥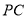 ,直线
,直线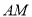 与直线
与直线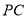 所成的角为60°.
所成的角为60°.
(1)求二面角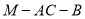 的的余弦值;
的的余弦值;
(2)求点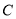 到面
到面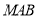 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:填空题
一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出 人.
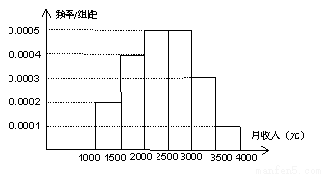
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:填空题
如图,在△ABC中,BO为边AC上的中线,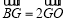 ,设
,设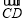 ∥
∥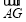 ,若
,若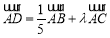
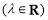 ,则
,则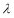 的值为 .
的值为 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏锡常镇四市高三教学情况调研二数学试卷(解析版) 题型:填空题
“ ”是“函数
”是“函数 的图象关于y轴对称”的
的图象关于y轴对称”的
条件.(在“充分必要”、“充分不必要”、“必要不充分”、
“既不充分也不必要”中选一个合适的填空)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com