
| A�� | 30�� | B�� | 60�� | C�� | 120�� | D�� | 150�� |
���� ����ƽ����������������нǹ�ʽ�����������Ӧ�Ľ����
��� �⣺��$\overrightarrow{{e}_{1}}$��$\overrightarrow{{e}_{2}}$�ļн�Ϊ�ȣ�
��$\overrightarrow{e_1}��\overrightarrow{e_2}$Ϊ��λ��������$\overrightarrow{e_1}$��$\overrightarrow{e_1}+2\overrightarrow{e_2}$��ֱ��
��$\overrightarrow{{e}_{1}}$•��$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$��=${\overrightarrow{{e}_{1}}}^{2}$+2$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=12+2��1��1��cos��=0��
���cos��=-$\frac{1}{2}$��
�֦ȡ�[0�㣬120��]��
$\overrightarrow{e_1}��\overrightarrow{e_2}$�ļн�Ϊ��=120�㣮
��ѡ��C��
���� ���⿼����ƽ����������������нǹ�ʽ��Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬѧ������������Ҫ��������� | B�� | ������һ����������� | ||
| C�� | ������һ��ֱ�������� | D�� | ������һ���۽������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
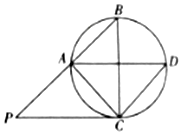 ��ͼ����P�ǡ�ABC���ԲԲO��C�������������AB�Ľ��㣮
��ͼ����P�ǡ�ABC���ԲԲO��C�������������AB�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
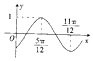 ��֪����f��x��=sin����x+�գ����أ�0���У�|��|����2�У��IJ���ͼ����ͼ��ʾ����յ�ֵΪ��������
��֪����f��x��=sin����x+�գ����أ�0���У�|��|����2�У��IJ���ͼ����ͼ��ʾ����յ�ֵΪ��������| A�� | $\frac{5��}{3}$ | B�� | $\frac{4��}{3}$ | C�� | -$\frac{4��}{3}$ | D�� | -$\frac{5��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\root{3}{x^3}$ | B�� | $y={��\sqrt{x}��^2}$ | C�� | $y=\sqrt{x^2}$ | D�� | $y=\frac{x^2}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com