
【题目】如果一个四面体的三个面是直角三角形,下列三角形:(1)直角三角形;(2)锐角三角形;(3)钝角三角形;(4)等腰三角形;(5)等腰直角三角形.那么可能成为这个四面体的第四个面是_____.(填上你认为正确的序号)
【答案】(1)(2)(4)(5)
【解析】
画出图像,根据四面体有三个面是直角三角形,结合图像,由此确定正确说法的序号.
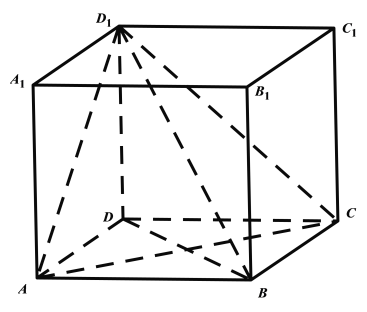
一个四面体的三个面是直角三角形,画出图像如图所示.
在长方体![]() 中,
中,![]() 是有三个面是直角三角形的四面体.
是有三个面是直角三角形的四面体.
当长方体![]() 的边长都相等时,三角形
的边长都相等时,三角形![]() 的边长也相等,为等比三角形,所以(2)(4)正确.
的边长也相等,为等比三角形,所以(2)(4)正确.
在长方体![]() 中,
中,![]() 是有四个面是直角三角形的四面体.当
是有四个面是直角三角形的四面体.当![]() 时,
时,![]() 为等腰直角三角形.
为等腰直角三角形.
所以(1)(5)正确.
在长方体![]() 中,
中,![]() 是有三个面是直角三角形的四面体.设
是有三个面是直角三角形的四面体.设![]() ,则
,则![]() ,
,![]() 任意两边的平方和,都大于第三边的平方,根据余弦定理可知
任意两边的平方和,都大于第三边的平方,根据余弦定理可知![]() 不是钝角三角形.结合上述分析可知,第四个面不可能是钝角三角形,所以(3)错误.
不是钝角三角形.结合上述分析可知,第四个面不可能是钝角三角形,所以(3)错误.
故答案为:(1)(2)(4)(5).


科目:高中数学 来源: 题型:
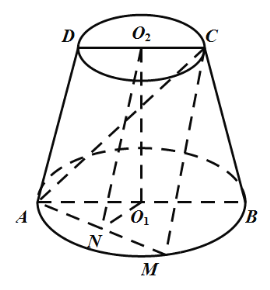
【题目】如图,在圆台![]() 中,平面
中,平面![]() 过上下底面的圆心
过上下底面的圆心![]() ,
,![]() ,点M在
,点M在![]() 上,N为
上,N为![]() 的中点,
的中点,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,
时,![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
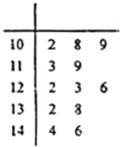
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员![]() 需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员
需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员![]() 获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{bn}的前n项和为Tn,且T4=4,b5=6.
(1)求数列{bn}的通项公式;
(2)若正整数n1,n2,…,nt,…满足5<n1<n2<…<nt,…且b3,b5,![]() ,
,![]() ,…,
,…,![]() ,…成等比数列,求数列{nt}的通项公式(t是正整数);
,…成等比数列,求数列{nt}的通项公式(t是正整数);
(3)给出命题:在公比不等于1的等比数列{an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1也成等差数列.试判断此命题的真假,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足,当点
为垂足,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交曲线
垂直的直线交曲线![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取得最小值时直线
面积的最小值,以及取得最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年11月河南省三门峡市成功入围“十佳魅力中国城市”,吸引了大批投资商的目光,一些投资商积极准备投入到“魅力城市”的建设之中.某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中.
项目一:天坑院是黄土高原地域独具特色的民居形式,是人类“穴居”发展史演变的实物见证.现准备投资建设20个天坑院,每个天坑院投资0.2百万元,假设每个天坑院是否盈利是相互独立的,据市场调研,到2020年底每个天坑院盈利的概率为![]()
![]() ,若盈利则盈利投资额的40%,否则盈利额为0.
,若盈利则盈利投资额的40%,否则盈利额为0.
项目二:天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区.据市场调研,投资到该项目上,到2020年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为p和![]() .
.
(1)若投资项目一,记![]() 为盈利的天坑院的个数,求
为盈利的天坑院的个数,求![]() (用p表示);
(用p表示);
(2)若投资项目二,记投资项目二的盈利为![]() 百万元,求
百万元,求![]() (用p表示);
(用p表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图数表:

每一行都是首项为1的等差数列,第![]() 行的公差为
行的公差为![]() ,且每一列也是等差数列,设第
,且每一列也是等差数列,设第![]() 行的第
行的第![]() 项为
项为![]() .
.
(1)证明:![]() 成等差数列,并用
成等差数列,并用![]() 表示
表示![]() (
(![]() );
);
(2)当![]() 时,将数列
时,将数列![]() 分组如下:(
分组如下:(![]() ),(
),(![]() ),(
),(![]() ),…(每组数的个数构成等差数列). 设前
),…(每组数的个数构成等差数列). 设前![]() 组中所有数之和为
组中所有数之和为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,设![]() 是不超过20的正整数,当
是不超过20的正整数,当![]() 时,求使得不等式
时,求使得不等式![]() 恒成立的所有
恒成立的所有![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com