
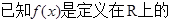 单调函数,
单调函数,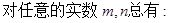

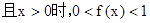 .
.
(1)证明:f(0)=1且x<0时f(x)>1;
(2)

(1)见解析(2)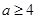
【解析】本试题主要是考查了抽象函数性质的运用。
(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)= f(0)= f(x)·f(–x)=1
∴f(x)=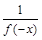 >1, 即x<0时,f(x)>1
>1, 即x<0时,f(x)>1
(2)
∴f(x)是定义域R上的单调递减函数
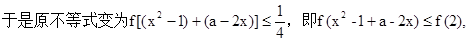 ,然后解不等式得到。
,然后解不等式得到。
解析:(1)在f(m+n)=f(m)·f(n)中,取m>0,n=0,有f(m)=f(m)·f(0) ,
∵x>0时0<f(x)<1 ∴f(0)=1 ………3分
又设m=x<0,n=–x>0 则0<f(–x)<1
∴f(m+n)= f(0)= f(x)·f(–x)=1
∴f(x)=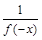 >1, 即x<0时,f(x)>1………6分
>1, 即x<0时,f(x)>1………6分
(2)
∴f(x)是定义域R上的单调递减函数. ………8分
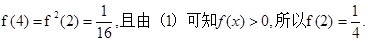 ………9分
………9分
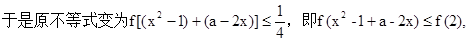 ………10分
………10分
 …11分
…11分
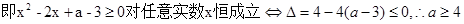 ………13分
………13分


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 2 |
| θ |
| 2 |
| b |
| 2 |
| θ |
| 2 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知y=f(x)是定义在R上的单调函数,实数x1≠x2,λ≠-1,α=![]() ,β=
,β=![]() ,若|f(x1)-f(x2)|<
,若|f(x1)-f(x2)|<
|f(α)-f(β)|,则( )
A.λ<0 B.λ=0 C.0<λ<1 D.λ≥1
查看答案和解析>>
科目:高中数学 来源: 题型:
对于函数f(x)=bx3+ax2-3x.
(1)若f(x)在x=1和x=3处取得极值,且f(x)的图象上每一点的切线的斜率均不超过2sintcost-2![]() cos2t+
cos2t+![]() ,试求实数t的取值范围;
,试求实数t的取值范围;
(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所围成的图形的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com