
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
【答案】
(1)
证明:取BC中点E,连结EN,EM,
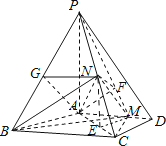
∵N为PC的中点,∴NE是△PBC的中位线,
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE= ![]() BC=AM=2,
BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN平面NEM,∴MN∥平面PAB
(2)
解:在△AMC中,由AM=2,AC=3,cos∠MAC= ![]() ,得CM2=AC2+AM2﹣2ACAMcos∠MAC=9+4-
,得CM2=AC2+AM2﹣2ACAMcos∠MAC=9+4- ![]() =5.
=5.
∴AM2+MC2=AC2,则AM⊥MC,
∵PA⊥底面ABCD,PA平面PAD,
∴平面ABCD⊥平面PAD,且平面ABCD∩平面PAD=AD,
∴CM⊥平面PAD,则平面PNM⊥平面PAD.
在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.
在Rt△PAC中,由N是PC的中点,得AN= ![]() ,
,
在Rt△PAM中,由PAAM=PMAF,得AF= ![]() ,
,
∴ 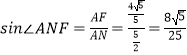 .
.
∴直线AN与平面PMN所成角的正弦值为 ![]()
【解析】(1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG= ![]() BC,再由已知得AM∥BC,且AM=
BC,再由已知得AM∥BC,且AM= ![]() BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;
BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;
法二、证明MN∥平面PAB,转化为证明平面NEM∥平面PAB,在△PAC中,过N作NE⊥AC,垂足为E,连接ME,由已知PA⊥底面ABCD,可得PA∥NE,通过求解直角三角形得到ME∥AB,由面面平行的判定可得平面NEM∥平面PAB,则结论得证;
(2)连接CM,证得CM⊥AD,进一步得到平面PNM⊥平面PAD,在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.然后求解直角三角形可得直线AN与平面PMN所成角的正弦值.本题考查直线与平面平行的判定,考查直线与平面所成角的求法,考查数学转化思想方法,考查了空间想象能力和计算能力,是中档题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2﹣ex,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求函数f(x)的单调区间;
(Ⅱ)试确定a的取值范围,使得曲线y=f(x)上存在唯一的点P,曲线在该点处的切线与曲线只有一个公共点P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解开展校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100] |
频数 | 6 | a | 24 | b |

(1)求a,b,c的值;
(2)先用分层抽样的方法从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈,再从这10人中任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(3)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校开展安全教育活动的成效.若
的方差)来评估该校开展安全教育活动的成效.若![]() ≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.
≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形. 
(1)证明:PB⊥CD;
(2)求二面角A﹣PD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}的首项为a1 , 公差为﹣1的等差数列,Sn为其前n项和,若S1 , S2 , S4成等比数列,则a1=( )
A.2
B.﹣2
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() a,曲线C2的参数方程为
a,曲线C2的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)求C1的直角坐标方程;
(2)当C1与C2有两个公共点时,求实数a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com