
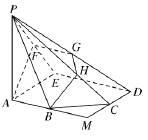
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 分别为线段
分别为线段![]() 的中点,在五棱锥
的中点,在五棱锥![]() 中,
中,![]() 为棱
为棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 分别交于点
分别交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() 底面
底面![]() ,且
,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要结合平几条件,如本题利用正方形性质得![]() ,从而有
,从而有![]() 平面
平面![]() .而线线平行的证明,一般利用线面平行性质定理,即从两平面交线出发给予证明(2)利用空间向量解决线面角,一般先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,再根据向量数量积求夹角,最后根据线面角与向量夹角之间互余关系求大小.
.而线线平行的证明,一般利用线面平行性质定理,即从两平面交线出发给予证明(2)利用空间向量解决线面角,一般先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,再根据向量数量积求夹角,最后根据线面角与向量夹角之间互余关系求大小.
试题解析:解:(1)证明:在正方形![]() 中,因为
中,因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,所以
,所以![]()
(2)因为![]() 底面
底面![]() ,所以
,所以![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则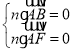 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则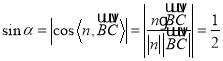 ,
,
因此直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]()


科目:高中数学 来源: 题型:
【题目】已知y=f(x),x∈(-a,a),F(x)=f(x)+f(-x),则F(x)是( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
,且![]() (如图1). 将四边形
(如图1). 将四边形![]() 沿
沿![]() 折起,连结
折起,连结![]() (如图2). 在折起的过程中,下列说法中错误的个数是( )
(如图2). 在折起的过程中,下列说法中错误的个数是( )
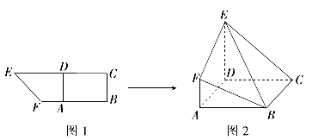
①![]() 平面
平面![]() ;
;
②![]() 四点不可能共面;
四点不可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.
可能垂直.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件ACB的集合C的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300km的海面
方向300km的海面![]() 处,并以20km/h的速度向西偏北
处,并以20km/h的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风侵袭的时间有多少小时?
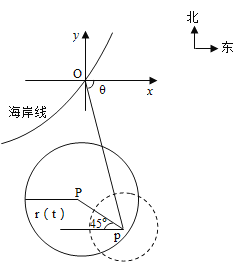
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com