
【题目】设定义在![]() 上的函数
上的函数![]() 对于任意实数
对于任意实数![]() ,都有
,都有![]() 成立,且
成立,且![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的单调性,并加以证明;
的单调性,并加以证明;
(2)试问:当![]() 时,
时,![]() 是否有最值?如果有,求出最值;如果没有,说明理由;
是否有最值?如果有,求出最值;如果没有,说明理由;
(3)解关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
【答案】(1)![]() 在
在![]() 上是减函数,证明见解析;(2)
上是减函数,证明见解析;(2)![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ;(3)当
;(3)当![]() 时,不等式的解集为
时,不等式的解集为![]() 或
或![]() ,当
,当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.
【解析】
试题分析:(1)任意实数![]() ,且
,且![]() ,不妨设
,不妨设![]() ,利用差比较法,计算
,利用差比较法,计算![]() ,所以函数为减函数;(2)
,所以函数为减函数;(2)![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 有最大值
有最大值![]() ,有最小值
,有最小值![]() .利用赋值法求出
.利用赋值法求出![]() ;(3)化简不等式得
;(3)化简不等式得![]() ,由于
,由于![]() 为减函数,所以
为减函数,所以![]() ,
,![]() .由于
.由于![]() ,
,![]() 或
或![]() ,所以当
,所以当![]() 时,
时,![]() ,不等式的解集为
,不等式的解集为![]() 或
或![]() ;当
;当![]() 时,
时,![]() ,不等式的解集为
,不等式的解集为![]() .
.
试题解析:
(1)![]() 在
在![]() 上是减函数,证明如下:对任意实数
上是减函数,证明如下:对任意实数![]() ,且
,且![]() ,不妨设
,不妨设![]() ,其中
,其中![]() ,则
,则![]() ,
,
∴![]() .故
.故![]() 在
在![]() 上单调递减.………………4分
上单调递减.………………4分
(2)∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() 时,
时,![]() 有最大值
有最大值![]() ,
,![]() 时,
时,![]() 有最小值
有最小值![]() .在
.在![]() 中,令
中,令![]() ,得
,得![]() ,
,
故![]() ,
,![]() ,所以
,所以![]() .
.
故当![]() 时,
时,![]() 的最大值是3,最小值是0.………………6分
的最大值是3,最小值是0.………………6分
(3)由原不等式,得![]() ,
,
由已知有![]() ,即
,即![]() .
.
∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,∴
,∴![]() .………………9分
.………………9分
∵![]() ,∴
,∴![]() 或
或![]() .
.
当![]() 时,
时,![]() ,不等式的解集为
,不等式的解集为![]() 或
或![]() ;
;
当![]() 时,
时,![]() ,不等式的解集为
,不等式的解集为![]() .………………12分
.………………12分


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:
【题目】为了参加市高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出![]() 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和.
项的和.
(1)若数列![]() 为等差数列.
为等差数列.
①求数列的通项![]() ;
;
②若数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() ,试比较数列
,试比较数列![]() 前
前![]() 项和
项和![]() 与
与![]() 前
前![]() 项和
项和![]() 的大小;
的大小;
(2)若对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)点P在直线l:2x-4y+3=0上,过点P作圆C的切线,切点记为M,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,射影定理可表示为a=b·cosC+c·cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某测观点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点与两焦点构成的三角形为正三角形.
,上顶点与两焦点构成的三角形为正三角形.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的内切圆的面积的最大值为
的内切圆的面积的最大值为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
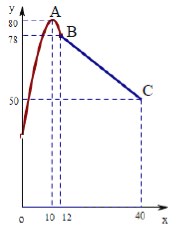
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com