
【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
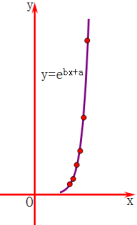
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
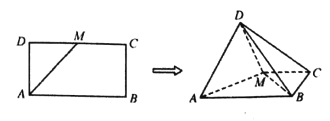
(1)当AB=2时,求三棱锥![]() 的体积;
的体积;
(2)求证:BM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且
的左、右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上任意一点,以
为椭圆上任意一点,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当圆
,当圆![]() 与直线
与直线![]() :
:![]() 有公共点时,求
有公共点时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合![]() ,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
(1)求A∩UB;
(2)若C(A∪B),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
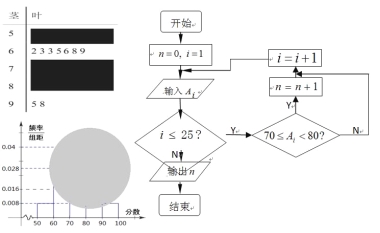
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com