练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数.

    （I）将写成的形式，并求其图象对称中心的横坐标；

    （II）如果△ABC的三边a、b、c满足b2= a c，且边b所对的角为，试求的范围及此时函数的值域.

    （I）对称中心的横坐标为，(k∈Z).  

    （II）0＜x≤.  f(x)的值域为（2，１+）.     


    解析:

    （I）f(x) =+(1+)=++

      =sin(+)+.由sin(+)= 0，即+=kπ(k∈Z)，

    得x=(k∈Z)，即对称中心的横坐标为，(k∈Z).  

    （II）由已知b2=ac，得cosx=≥.

    ∴≤cosx＜1，0＜x≤.   

    ∴＜+≤.∵＞，

    ∴sin＜sin(+)≤1. +<sin(+)+≤１+,

    即f(x)的值域为（2，１+）.      

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012-2013学年山东省济宁市高三（上）期末数学试卷（文科）（解析版） 题型：解答题

    已知函数．
    （I）求函数f（x）的最小正周期和单调递增区间；
    （II）将函数y=f（x）的图象上各点的纵坐标保持不变，横坐标缩短到原来的，再把所得到的图象向左平移个单位长度，得到函数y=g（x）的图象，求函数y=g（x）在区间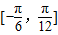上的值域．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年安徽省安庆市望江二中高三（上）第三次月考数学试卷（理科）（解析版） 题型：解答题

    已知函数．
    （I）求f（x）的最小正周期；
    （Ⅱ）若将f（x）的图象按向量=（，0）平移得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省德州市重点中学高三（上）10月月考数学试卷（理科）（解析版） 题型：解答题

    已知函数．
    （I）求f（x）的最小正周期；
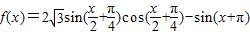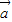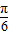    （Ⅱ）若将f（x）的图象按向量=（，0）平移得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：2013年安徽省池州市东至县高考数学一模试卷（理科）（解析版） 题型：解答题

    已知函数．
    （I）求f（x）的最小正周期；
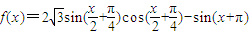    （Ⅱ）若将f（x）的图象按向量=（，0）平移得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省四地六校联考高三上学期第二次月考文科数学卷 题型：解答题

    （本小题满分12分）

    已知函数．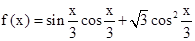

    （I）将函数f(x)写成f(x)=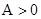（）的形式，并求其图像对称中心的横坐标；

    （Ⅱ）如果△ABC的三边a、b、c所对的角分别为A ,B ,C且满足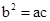，且边b所对的角为B，试求角B的取值范围及此时函数f(B)的值域.

     

    查看答案和解析>>

    同步练习册答案