
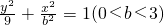 的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心.
的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心.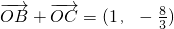 ,求椭圆的方程和直线BC的方程.
,求椭圆的方程和直线BC的方程. ,
,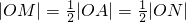 ,
, ,点N的坐标为
,点N的坐标为 ,
, ,(9分)
,(9分) ,
,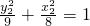 ,
, ,相减得,
,相减得,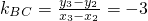 ,(11分)
,(11分) ,即6x+2y-9=0.(12分)
,即6x+2y-9=0.(12分) ,再由a=3能导出|AF|+|BF|+|CF|的值.
,再由a=3能导出|AF|+|BF|+|CF|的值.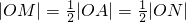 ,又|BM|=|MC|,所以四边形OBNC为平行四边形,由此入手能够得到椭圆的方程和直线BC的方程.
,又|BM|=|MC|,所以四边形OBNC为平行四边形,由此入手能够得到椭圆的方程和直线BC的方程.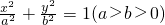 上一点,则P到左焦点F1与到右焦点F2的距离即焦半径分别为|PF1|=a+ex,|PF2|=a-ex;若P(x,y)为椭圆
上一点,则P到左焦点F1与到右焦点F2的距离即焦半径分别为|PF1|=a+ex,|PF2|=a-ex;若P(x,y)为椭圆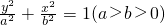 上一点,则P到下焦点F1与到上焦点F2的距离即焦半径分别为|PF1|=a+ey,|PF2|=a-ey;(2)设A(x1,y1),B(x2,y2),C(x3,y3),则三角形△ABC重心坐标公式
上一点,则P到下焦点F1与到上焦点F2的距离即焦半径分别为|PF1|=a+ey,|PF2|=a-ey;(2)设A(x1,y1),B(x2,y2),C(x3,y3),则三角形△ABC重心坐标公式 ,
, ;(3)设椭圆方程为:
;(3)设椭圆方程为: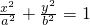 (a>b>0),kAB表示椭圆以A(x1,y1),B(x2,y2)为端点的弦AB的斜率,令M(X0,Y0)为弦AB的中点,M与椭圆中心O连线的斜率为kOM,则有
(a>b>0),kAB表示椭圆以A(x1,y1),B(x2,y2)为端点的弦AB的斜率,令M(X0,Y0)为弦AB的中点,M与椭圆中心O连线的斜率为kOM,则有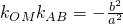 ;对于双曲线:
;对于双曲线: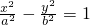 (a>0,b>0),同理可得
(a>0,b>0),同理可得 ;对于抛物线x2=±2py或y2=±2px,也可有
;对于抛物线x2=±2py或y2=±2px,也可有 或
或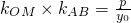 .在研究直线与二次曲线问题时,将这结论适当加以应用,常会使问题的解决变得很简便.
.在研究直线与二次曲线问题时,将这结论适当加以应用,常会使问题的解决变得很简便. 

科目:高中数学 来源: 题型:
| y2 |
| 9 |
| x2 |
| b2 |
| OB |
| OC |
| 8 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| A、9 | B、15 | C、12 | D、8 |
查看答案和解析>>
科目:高中数学 来源:2010年全国高考数学模拟试卷(1)(解析版) 题型:解答题
 的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心.
的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心. ,求椭圆的方程和直线BC的方程.
,求椭圆的方程和直线BC的方程.查看答案和解析>>
科目:高中数学 来源:2010年全国高考数学模拟试卷4(文理合卷)(解析版) 题型:解答题
 的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心.
的内接三角形,F是椭圆的上焦点,且原点O是△ABC的重心. ,求椭圆的方程和直线BC的方程.
,求椭圆的方程和直线BC的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com