
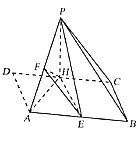
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.
(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
【答案】(1)见解析;(2)a=2
【解析】
(1)分别证明EH∥平面PBC和EF∥平面PBC,再由EF∩EH=E,即可证明结论;
(2)根据条件求出AH![]() ,DH=PH=CH
,DH=PH=CH![]() ,然后证明PH⊥平面ABCH,又点F为AP的中点,则S△PEF=S△AEF,故VH-PEF=VH-AEF,则
,然后证明PH⊥平面ABCH,又点F为AP的中点,则S△PEF=S△AEF,故VH-PEF=VH-AEF,则![]() ,据此计算求解即可.
,据此计算求解即可.
(1)证明:菱形ABCD中,∵E,H分别为AB,CD的中点,∴BE∥CH,BE=CH,
∴四边形BCHE为平行四边形,则BC∥EH,又EH平面PBC,∴EH∥平面PBC,
又点E,F分别为AB,AP的中点,则EF∥BP,又EF平面PBC,∴EF∥平面PBC,
由EF∩EH=E,∴平面EFH∥平面PBC;
(2)在菱形ABCD中,∠D=60°,则△ACD为正三角形,
∴AH⊥CD,AH![]() ,DH=PH=CH
,DH=PH=CH![]() ,
,
折叠后,PH⊥AH,又平面PHA⊥平面ABCH,平面PHA∩平面ABCH=AH,从而PH⊥平面ABCH.
在△PAE中,点F为AP的中点,则S△PEF=S△AEF,∴VH-PEF=VH-AEF,
而VH-PEF+VH-AEF=VH-PAE,
∴![]()
![]() ,
,
∴a3=8,即a=2.故a=2.


科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: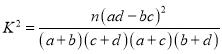
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com