
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
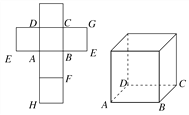
【答案】(1)见解析;(2)平面BEG∥平面ACH;(3)证明见解析
【解析】试题分析:(1)折叠成正方体即可得出;(2)根据条件可证四边形BCEH为平行四边形,因此BE∥CH,由线面平行判定定理即可得证;(3)根据DH⊥平面EFGH可得DH⊥EG,又EG⊥FH,可证EG⊥平面BFHD,所以DF⊥EG,同理可证同理DF⊥BG,所以命题得证.
试题解析:
(1)点F、G、H的位置如图所示.
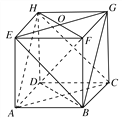
(2)平面BEC∥平面ACH.证明如下:
因为ABCD-EFGH为正方体,所以BC∥FG,BC=FG,
又FG∥EH,FG=EH,所以BC∥EH,BC=EH,
于是四边形BCEH为平行四边形,
所以BE∥CH,
又CH平面ACH,BE平面ACH,
所以BE∥平面ACH,
同理,BG∥平面ACH,
又BE∩BG=B,
所以平面BEG∥平面ACH.
(3)连接FH交EG于点O,连接BD.
因为ABCD-EFGH为正方体,所以DH⊥平面EFGH,
因为EG平面EFGH,所以DH⊥EG,
又EG⊥FH,EG∩FH=O,
所以EG⊥平面BFHD,
又DF平面BFHD,所以DF⊥EG,
同理DF⊥BG,
又EG∩BG=G,
所以DF⊥平面BEG.


科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是 ( )
A. l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B. l1的斜率为-![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q![]()
C. l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2![]() )
)
D. l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.
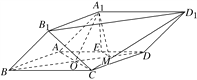
(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线a,b和平面M,N,且a⊥M,则下列说法正确的是 ( )
A. b∥Mb⊥a B. b⊥ab∥M
C. N⊥Ma∥N D. aNM∩N≠
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
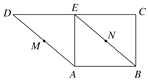
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣alnx(a∈R)
x2﹣alnx(a∈R)
(1)若函数f(x)在x=2处的切线方程为y=x+b,求a,b的值;
(2)讨论方程f(x)=0解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|)。
(1)求实数a,b的值;
(2)若不等式f(2k)>1成立,求实数k的取值范围;
(3)定义在[p,q]上的函数![]() (x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
(x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() (x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
(x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com