
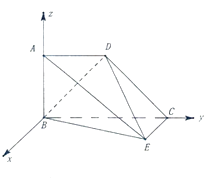
【题目】如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB,已知BC=2AD=2AB=2. 
(1)证明:BD⊥平面DEC;
(2)若二面角A﹣ED﹣B的大小为30°,求EC的长度.
【答案】
(1)证明:∵AB⊥平面BEC,∴AB⊥EC,
又∵EC⊥BC,AB∩BC=B,∴EC⊥平面ABCD,
∵BD平面ABCD,∴EC⊥BD,
由题意知在梯形ABCD中,有BD=DC= ![]() ,
,
∴BD2+DC2=BC2,∴BD⊥DC,
又EC∩CD=C,∴BD⊥平面DEC.
(2)解:如图,以B为原点,在平面BCE中过B作BC的垂线为x轴,
BC为y轴,BA为z轴,建立空间直角坐标系,
设 ![]() =a>0,则B(0,0,0),E(a,2,0),A(0,0,1),C(0,2,0),D(0,1,1),
=a>0,则B(0,0,0),E(a,2,0),A(0,0,1),C(0,2,0),D(0,1,1),
![]() =(0,1,0),
=(0,1,0), ![]() =(﹣a,﹣1,1),
=(﹣a,﹣1,1),
设面AED的法向量为 ![]() =(x,y,z),
=(x,y,z),
则  ,令x=1,得
,令x=1,得 ![]() =(1,0,a),
=(1,0,a),
设面BED的法向量为 ![]() =(x1,y1,z1),
=(x1,y1,z1),
则  ,令x1=2,得
,令x1=2,得 ![]() =(2,﹣a,a),
=(2,﹣a,a),
∵二面角A﹣ED﹣B的大小为30°,
∴cos30°= ![]() =
= ![]() =
= ![]() ,解得a=1.(a=﹣1,舍),
,解得a=1.(a=﹣1,舍),
∴EC=1.
【解析】(1)推导出AB⊥EC,EC⊥BC,从而EC⊥平面ABCD,进而EC⊥BD,由勾股定理得BD⊥DC,由此能证明BD⊥平面DEC.(2)以B为原点,在平面BCE中过B作BC的垂线为x轴,BC为y轴,BA为z轴,建立空间直角坐标系,利用向量法能求出EC.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE. 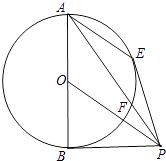
(1)求证:PE是圆O的切线;
(2)设AO=3,PB=4,求PF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m与α所成的角和n与β所成的角相等.
其中正确的命题有.(填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1.
(1)求a,b的值;
(2)设 ![]() ,若关于x的方程
,若关于x的方程 ![]() 在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,求实数k的取值范围.
在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn , 则下列不可能成立的( )
A.a2016(S2016﹣S2015)=0
B.a2016(S2016﹣S2014)=0
C.(a2016﹣a2013)(S2016﹣S2013)=0
D.(a2016﹣a2012)(S2016﹣S2012)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线C: ![]() =1(a>0,b>0)的左、右焦点,其离心率为e,点B的坐标为(0,b),直线F1B与双曲线C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴,直线F1B的交点分别为M,R,若△RMF1与△PQF2的面积之比为e,则双曲线C的离心率为( )
=1(a>0,b>0)的左、右焦点,其离心率为e,点B的坐标为(0,b),直线F1B与双曲线C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴,直线F1B的交点分别为M,R,若△RMF1与△PQF2的面积之比为e,则双曲线C的离心率为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆 ![]() 的左、右焦点,F2在以
的左、右焦点,F2在以 ![]() 为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a. 
(1)求椭圆C1的方程;
(2)过点P(0,1)的直线l1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆C2于C,D两点,M为线段CD中点,求△MAB面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn , Tn分别是数列{an},{bn}的前n项和,已知对于任意n∈N* , 都有3an=2Sn+3,数列{bn}是等差数列,且T5=25,b10=19. (Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn= ![]() ,求数列{cn}的前n项和Rn , 并求Rn的最小值.
,求数列{cn}的前n项和Rn , 并求Rn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解,记实数m的最大值为M.
(1)求M的值;
(2)正数a,b,c满足a+2b+c=M,求证: ![]() +
+ ![]() ≥1.
≥1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com