【题目】已知在△ABC中，三条边
所对的角分别为A、B，C，向量
=（
），
=（
），且满足=
．
（1）求角C的大小；
（2）若sinA，sinC，sinB成等比数列，且
=﹣8，求边
的值并求△ABC外接圆的面积．
【答案】（1）
（2）
【解析】试题分析：（1）由向量的数量积公式和向量
的坐标，可知sin（A+B）=2sinCcosC，所以cosC=
，
，可解得C=
。（2）由等比数列可得sin2C=sinAsinB，代入正弦定理可得c2=ab，由数量积可得
=﹣8，所以ab=16，c=4,由正弦定理
，可求得外接圆半径。
试题解析：（1）∵向量
=（sinA，cosA），
=（cosB，sinB），且满足=sin2C，
∴sin（A+B）=2sinCcosC，
∴cosC=，∴C=；
（2）∵sinA，sinC，sinB成等比数列
∴sin2C=sinAsinB，∴c2=ab，
∵
（
﹣）=﹣8，∴=﹣8，∴ab=16，∴c=4，
设外接圆的半径为R，由正弦定理可知：2R=
∴R=
，∴S=
．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数
（
为常数，
=2.71828……是自然对数的底数），曲线
在点
处的切线与
轴平行．
（1）求的值；
（2）求
的单调区间；
（3）设
，其中
是的导函数．证明：对任意
＞0，
＜
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】否定“自然数
、
、
中恰有一个偶数”时正确的反设为（ ）
A. 
、
、
都是奇数 B. 
、
、
至少有两个偶数
C. 
、
、
都是偶数 D. 
、
、
中都是奇数或至少有两个偶数
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次购物抽奖活动中，假设某10张券中有一等奖1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有将；某顾客从此10张券中任取2张，求：
（1）该顾客中奖的概率；
（2）该顾客获得的奖品总价值
（元）的概率分布列.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学为了解2017届高三学生的性别和喜爱游泳是否有关，对100名高三学生进行了问卷调查，得到如下列联表：
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为
．
（Ⅰ）请将上述列联表补充完整；
（Ⅱ）判断是否有99.9%的把握认为喜欢游泳与性别有关？
附：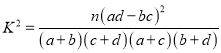 
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
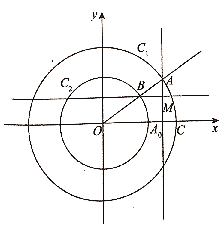
【题目】如图所示，以原点
为圆心的两个同心圆
，其中，大圆
的半径为
，小圆的半径为
，点
为大圆
上一动点，连接
，与小圆
交于点
，过点
作
轴的垂线，垂足为
，过点
作直线
的垂线，垂足为
，点
，记
.
（1）求点
的坐标（用含有
的式子表示），并写出点
的轨迹方程，指出点
的轨迹是什么曲线；
（2）设点
的轨迹为
，点
分别是曲线
上的两个动点，且
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-5：不等式选讲
已知函数f（x）=|2x＋1|+|2x－a|．
（I）若f（x）的最小值为2，求a的值；
（II）若f（x）≤|2x－4|的解集包含[－2，－1]，求a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
