
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ).
).
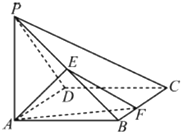
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果是,请证明;如果不是,请说明理由;
是否互相垂直?如果是,请证明;如果不是,请说明理由;
(2)求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
【答案】(1)平面![]() 平面
平面![]() ,理由见解析;(2)
,理由见解析;(2)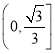
【解析】
(1)利用线面垂直的判定定理证明![]() 平面
平面![]() ,根据线面关系即可证明平面
,根据线面关系即可证明平面![]() 与平面
与平面![]() 垂直;
垂直;
(2)建立空间直角坐标系,根据平面![]() 与平面
与平面![]() 法向量的夹角的余弦的取值范围,计算出二面角
法向量的夹角的余弦的取值范围,计算出二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
(1)因为![]() ,
,![]() 为线段
为线段![]() 的中点.所以
的中点.所以![]() .
.
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由题意,以![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() 轴建立空间直角坐标系如图所示,令
轴建立空间直角坐标系如图所示,令![]() ,
,

则![]() ,
,![]() ,
,![]() ,
,![]() (其中
(其中![]() ).易知平面
).易知平面![]() 的一个法向量
的一个法向量![]() .
.
设平面![]() 的法向量
的法向量![]() ,由
,由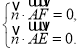 即
即![]()
令![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.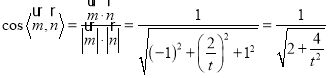 ,
,
由![]() ,所以
,所以![]() ,所以
,所以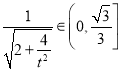 .
.
故若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ),二面角
),二面角![]() 的余弦值的取值范围是
的余弦值的取值范围是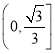 .
.


科目:高中数学 来源: 题型:
【题目】如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面a内作菱形ABCD,边长为1,∠BAD=60°,再在a的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.

(1)求二面角P-BD-Q的余弦值;
(2)求点P到平面QBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为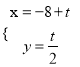 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为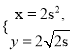 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
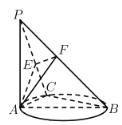
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月9-25日,第23届冬奥会在韩国平昌举行.4年后,第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人?
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com