
【题目】在实数![]() 中定义一种新运算:
中定义一种新运算: ![]() ,对实数
,对实数![]() 经过运算
经过运算![]() 后是一个确定的唯一的实数。
后是一个确定的唯一的实数。![]() 运算有如下性质:(1)对任意实数
运算有如下性质:(1)对任意实数![]() ,
, ![]() ;(2)对任意实数
;(2)对任意实数![]() ,
, ![]() 那么:关于函数
那么:关于函数![]() 的性质下列说法正确的是:①函数
的性质下列说法正确的是:①函数![]() 的最小值为3;②函数
的最小值为3;②函数![]() 是偶函数;③函数
是偶函数;③函数![]() 在
在![]() 上为减函数,这三种说法正确的有__________.
上为减函数,这三种说法正确的有__________.
科目:高中数学 来源: 题型:
【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
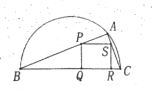
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在![]() 内的为青年教师,
内的为青年教师,![]() 内的为中年教师,
内的为中年教师,![]() 内的为老年教师.
内的为老年教师.
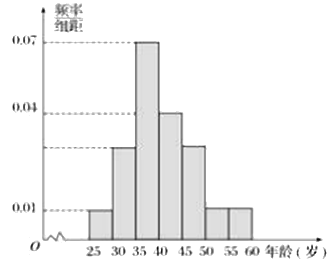
(1)求年龄![]() ,
,![]() 内的教师人数;
内的教师人数;
(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
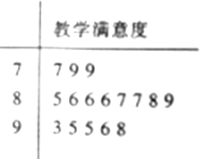
【题目】某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)若教学满意度不低于9.5分,则称该生对教师的教学满意度为“极满意”.求从这16人中随机选取3人,至少有1人是“极满意”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记![]() 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,小波从![]() 街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是
街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是![]() ,红灯亮的概率都是
,红灯亮的概率都是![]() .
.
(1)求小波遇到4次绿灯后,处于![]() 街区的概率;
街区的概率;
(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与![]() 街区相距的街道数为
街区相距的街道数为![]() (如小波若处在
(如小波若处在![]() 街区则相距零个街道,处在
街区则相距零个街道,处在![]() ,
,![]() 街区都是相距2个街道),求
街区都是相距2个街道),求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com