
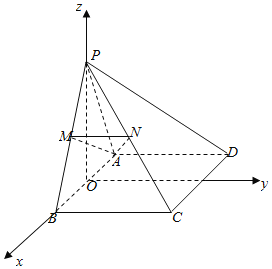
【题目】在四棱锥P—ABCD中,![]() PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.
PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.

(1)求证:MN//平面PAD;
(2)求二面角B—AM—C的大小;
(3)在BC上是否存在点E,使得EN⊥平面AMV?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
【答案】(1)证明见解析(2)45°(3)存在,![]()
【解析】
(1)欲证![]() //平面
//平面![]() ,则证明MN∥AD即可.
,则证明MN∥AD即可.
(2)取![]() 中点
中点![]() 再建立空间直角坐标系,求得
再建立空间直角坐标系,求得![]() 与
与![]() 的法向量再求解即可.
的法向量再求解即可.
(3)设![]() 再根据
再根据![]() 平面
平面![]() ,列出对应的向量,利用数量积为0,求出
,列出对应的向量,利用数量积为0,求出![]() 再计算即可.
再计算即可.
证明:(1)∵M,N分别是PB,PC中点
∴MN是△ABC的中位线
∴MN∥BC∥AD
又∵AD![]() 平面PAD,MN
平面PAD,MN![]() 平面PAD
平面PAD
所以MN∥平面PAD.
解:(2)过点P作PO垂直于AB,交AB于点O,
因为平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
如图建立空间直角坐标系,
设AB=2,则A(﹣1,0,0),C(1,1,0),
M(![]() ,0,
,0,![]() ),
),
B(1,0,0),N(![]() ),
),
则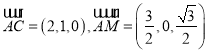
设平面CAM法向量为![]() ,
,
由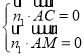 ,得
,得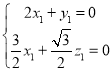 ,
,
令x1=1,则![]() ,即
,即![]()
平面ABM法向量![]()
所以,二面角B﹣AM﹣C的余弦值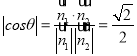
因为二面角B﹣AM﹣C是锐二面角,
所以二面角B﹣AM﹣C等于45°
(3)存在点E,使得EN⊥平面AMN
设E(1,λ,0),则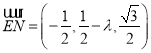 ,
,
由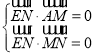 可得
可得![]() ,
,
所以在BC存在点E,使得EN⊥平面AMN,
此时![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数 ,关于
,关于![]() 的方程
的方程![]() ,给出下列结论
,给出下列结论
①存在这样的实数![]() ,使得方程有3个不同的实根
,使得方程有3个不同的实根
②不存在这样的实数![]() ,是的方程有4个不同的实根
,是的方程有4个不同的实根
③存在这样的实数![]() ,是的方程有5个不同的实根
,是的方程有5个不同的实根
④不存在这样的实数![]() ,是的方程有6个不同的实根
,是的方程有6个不同的实根
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间![]() 的长度均为
的长度均为![]() ,其中
,其中![]()
(1)若函数![]() 的定义域为
的定义域为![]() 值域为
值域为![]() 写出区间长度
写出区间长度![]() 的最大值;
的最大值;
(2)若关于![]() 的不等式组
的不等式组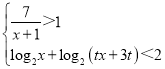 的解集构成的各区间长度和为6,求实数
的解集构成的各区间长度和为6,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 求证:关于
求证:关于![]() 的不等式
的不等式![]() 的解集构成的各区间的长度和为定值.
的解集构成的各区间的长度和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() ;
;
(1)若![]() ,求证:数列
,求证:数列![]() 是等差数列,并求此时数列
是等差数列,并求此时数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求证:数列
,求证:数列![]() 是等比数列,并求此时数列
是等比数列,并求此时数列![]() 的通项公式;
的通项公式;
(3)设![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面内一动点![]() 到两个定点
到两个定点![]() 、
、![]() 的距离之和为
的距离之和为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 在线段
在线段![]() 的上方,线段
的上方,线段![]() 的垂直平分线为
的垂直平分线为![]() .
.
①求![]() 的面积的最大值;
的面积的最大值;
②轨迹![]() 上是否存在除
上是否存在除![]() 、
、![]() 外的两点
外的两点![]() 、
、![]() 关于直线
关于直线![]() 对称,请说明理由.
对称,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为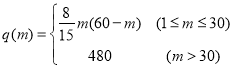 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①命题“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题
”是一个真命题
③“![]() 的否定是“
的否定是“![]() ”
”
④已知![]() ,
,![]() 都是实数,“
都是实数,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com