
ЁОЬтФПЁПЮЊКыбяУёзхЮФЛЏЃЌФГбЇаЃбЇЩњШЋдБВЮгыОйааСЫЁАЮвАЎЙњбЇЃЌДЋЫаОЕфЁБПМЪдЃЌВЂДгжаГщШЁ![]() УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉзїЮЊбљБОЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЎГЩМЈТфдк
УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉзїЮЊбљБОЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЎГЩМЈТфдк![]() жаЕФШЫЪ§ЮЊ20ЃЎ
жаЕФШЫЪ§ЮЊ20ЃЎ

ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉИљОнбљБОЙРМЦзмЬхЕФЫМЯыЃЌЙРМЦИУаЃбЇЩњЪ§бЇГЩМЈЕФЦНОљЪ§![]() КЭжаЮЛЪ§
КЭжаЮЛЪ§![]() ЃЛЃЈЭЌвЛзщЪ§ОнжаЕФЪ§ОнвдетзщЪ§ОнЫљдкЧјМфжаЕуЕФжЕзїДњБэЃЉ
ЃЛЃЈЭЌвЛзщЪ§ОнжаЕФЪ§ОнвдетзщЪ§ОнЫљдкЧјМфжаЕуЕФжЕзїДњБэЃЉ
ЃЈ3ЃЉШєГЩМЈдк80ЗжвдЩЯЃЈКЌ80ЗжЃЉЮЊЁАЙњбЇаЁДяШЫЁБЃЎШєдкбљБОжаЃЌРћгУЗжВуГщбљЕФЗНЗЈДгЁАЙњбЇаЁДяШЫЁБжаЫцЛњГщШЁ5ШЫЃЌдйДгжаГщШЁ2ШЫдљЫЭвЛЬзЙњбЇОЕфЃЌМЧЁАГщжаЕФ2УћбЇЩњГЩМЈЖМВЛЕЭгк90ЗжЁБЮЊЪТМў![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЛ
ЃЛ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ ЃЈ2ЃЉЦНОљЪ§ЮЊ
ЃЛ ЃЈ2ЃЉЦНОљЪ§ЮЊ![]() ЃЌжаЮЛЪ§ЮЊ
ЃЌжаЮЛЪ§ЮЊ![]() ЃЛ ЃЈ3ЃЉ
ЃЛ ЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМЕФаджЪФмЧѓГі![]() ЃЌдйгЩГЩМЈТфдк
ЃЌдйгЩГЩМЈТфдк![]() ЃЌ
ЃЌ![]() жаЕФЦЕТЪЮЊ
жаЕФЦЕТЪЮЊ![]() ЃЌФмЧѓГі
ЃЌФмЧѓГі![]() ЃЛ
ЃЛ
ЃЈ2ЃЉИљОнбљБОЙРМЦзмЬхЕФЫМЯыЃЌМДПЩЙРМЦИУаЃбЇЩњЪ§бЇГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉгЩЗжВуГщбљПЩЫуГіЃЌГЩМЈдк![]() ЃЌ
ЃЌ![]() жаГщШЁ3ШЫМЧЮЊ
жаГщШЁ3ШЫМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЃЌГЩМЈдк
ЃЌЃЌГЩМЈдк![]() ЃЌ
ЃЌ![]() жаГщШЁ2ШЫМЧЮЊ
жаГщШЁ2ШЫМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌРћгУСаОйЗЈЃЌвЛвЛСаГіДгет5ШЫжаГщШЁ2ШЫЕФЫљгаЛљБОЪТМўКЭЪТМўЕФ
ЃЌРћгУСаОйЗЈЃЌвЛвЛСаГіДгет5ШЫжаГщШЁ2ШЫЕФЫљгаЛљБОЪТМўКЭЪТМўЕФ![]() ЛљБОЪТМўЃЌРћгУЙХЕфИХаЭЧѓИХТЪМДПЩЧѓГі
ЛљБОЪТМўЃЌРћгУЙХЕфИХаЭЧѓИХТЪМДПЩЧѓГі![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ГщШЁ
ГщШЁ![]() УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉзїЮЊбљБОЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМЃЌ
УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉзїЮЊбљБОЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМЃЌ
ГЩМЈТфдк![]() ЃЌ
ЃЌ![]() жаЕФШЫЪ§ЮЊ20ЃЌ
жаЕФШЫЪ§ЮЊ20ЃЌ
ГЩМЈТфдк![]() ЃЌ
ЃЌ![]() жаЕФЦЕТЪЮЊ
жаЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
Ёр![]() .
.
ЃЈ2ЃЉгЩЬтвтЃЌИїзщЕФЦЕТЪЗжБ№ЪЧ0.05ЃЌ0.2ЃЌ0.5ЃЌ0.15ЃЌ0.1ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЕФЦЕТЪЮЊ
ЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЕФЦЕТЪЮЊ
ЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
![]() жаЮЛЪ§
жаЮЛЪ§![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЃЉГЩМЈдк80ЗжвдЩЯЃЈКЌ80ЗжЃЉЮЊЁАЙњбЇаЁДяШЫЁБЃЌ
дкбљБОжаЃЌРћгУЗжВуГщбљЕФЗНЗЈДгЁАЙњбЇаЁДяШЫЁБжаЫцЛњГщШЁ5ШЫЃЌ
дђГЩМЈдк![]() ЃЌ
ЃЌ![]() жаГщШЁ
жаГщШЁ![]() ШЫЃЌ
ШЫЃЌ
ГЩМЈдк![]() ЃЌ
ЃЌ![]() жаГщШЁ
жаГщШЁ![]() ШЫЃЌ
ШЫЃЌ
МЧГЩМЈдк![]() ЕФ3ШЫЮЊ
ЕФ3ШЫЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌГЩМЈдк
ЃЌГЩМЈдк![]() ЕФ2ШЫЮЊ
ЕФ2ШЫЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђДгет5ШЫжаГщШЁ2ШЫЕФЫљгаПЩФмНсЙћгаЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙВ10жжЃЎ
ЃЌЙВ10жжЃЎ
ЦфжаЪТМў![]() ЫљАќКЌЕФНсЙћга
ЫљАќКЌЕФНсЙћга![]() ЃЌ1жжНсЙћЃЌ
ЃЌ1жжНсЙћЃЌ
гЩЙХЕфИХаЭЧѓИХТЪЙЋЪНЕУЃК![]() ЃЎ
ЃЎ


 ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ УћаЃСЊУЫГхДЬОэЯЕСаД№АИ
УћаЃСЊУЫГхДЬОэЯЕСаД№АИ УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЛЧПЯеЪЧГЕжїБиаыЮЊЛњЖЏГЕЙКТђЕФЯежжЃЌШєЦеЭЈ6зљвдЯТЫНМвГЕЭЖБЃНЛЧПЯеЕквЛФъЕФЗбгУ(ЛљзМБЃЗб)ЭГвЛЮЊaдЊЃЌдкЯТвЛФъајБЃЪБЃЌЪЕааЕФЪЧЗбТЪИЁЖЏЛњжЦЃЌЧвБЃЗбгыЩЯвЛФъЖШГЕСОЗЂЩњЕРТЗНЛЭЈЪТЙЪЕФЧщПіЯрСЊЯЕЃЎЗЂЩњНЛЭЈЪТЙЪЕФДЮЪ§дНЖрЃЌЗбТЪвВОЭдНИпЃЌОпЬхИЁЖЏЧщПіШчЯТБэЃК
НЛЧПЯеИЁЖЏвђЫиКЭЗбТЪИЁЖЏБШТЪБэ | ||
ИЁЖЏвђЫи | ИЁЖЏБШТЪ | |
A1 | ЩЯвЛИіФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ | ЯТИЁ10% |
A2 | ЩЯСНИіФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ | ЯТИЁ20% |
A3 | ЩЯШ§ИіМАвдЩЯФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ | ЯТИЁ30% |
A4 | ЩЯвЛИіФъЖШЗЂЩњвЛДЮгад№ШЮВЛЩцМАЫРЭіЕФЕРТЗНЛЭЈЪТЙЪ | 0% |
A5 | ЩЯвЛИіФъЖШЗЂЩњСНДЮМАСНДЮвдЩЯгад№ШЮЕРТЗНЛЭЈЪТЙЪ | ЩЯИЁ10% |
A6 | ЩЯвЛИіФъЖШЗЂЩњгад№ШЮЕРТЗНЛЭЈЫРЭіЪТЙЪ | ЩЯИЁ30% |
ФГЛњЙЙЮЊСЫбаОПФГвЛЦЗХЦЦеЭЈ6зљвдЯТЫНМвГЕЕФЭЖБЃЧщПіЃЌЫцЛњГщШЁСЫ60СОГЕСфвбТњШ§ФъИУЦЗХЦЭЌаЭКХЫНМвГЕЕФЯТвЛФъајБЃЪБЕФЧщПіЃЌЭГМЦЕУЕНСЫЯТУцЕФБэИёЃК
РраЭ | A1 | A2 | A3 | A4 | A5 | A6 |
Ъ§СП | 10 | 5 | 5 | 20 | 15 | 5 |
(1)ЧѓвЛСОЦеЭЈ6зљвдЯТЫНМвГЕдкЕкЫФФъајБЃЪББЃЗбИпгкЛљБОБЃЗбЕФЦЕТЪЃЛ
(2)ФГЖўЪжГЕЯњЪлЩЬзЈУХЯњЪлетвЛЦЗХЦЕФЖўЪжГЕЃЌЧвНЋЯТвЛФъЕФНЛЧПЯеБЃЗбИпгкЛљБОБЃЗбЕФГЕСОМЧЮЊЪТЙЪГЕЃЎМйЩшЙКНјвЛСОЪТЙЪГЕПїЫ№5 000дЊЃЌвЛСОЗЧЪТЙЪГЕгЏРћ10 000дЊЃЎЧвИїжжЭЖБЃРраЭЕФЦЕТЪгыЩЯЪіЛњЙЙЕїВщЕФЦЕТЪвЛжТЃЌЭъГЩЯТСаЮЪЬтЃК
ЂйШєИУЯњЪлЩЬЕъФкга6СО(ГЕСфвбТњШ§Фъ)ИУЦЗХЦЖўЪжГЕЃЌФГЙЫПЭгћдкЕъФкЫцЛњЬєбЁ2СОГЕЃЌЧѓет2СОГЕЧЁКУгавЛСОЮЊЪТЙЪГЕЕФИХТЪЃЛ
ЂкШєИУЯњЪлЩЬвЛДЮЙКНј120СО(ГЕСфвбТњШ§Фъ)ИУЦЗХЦЖўЪжГЕЃЌЧѓвЛСОГЕгЏРћЕФЦНОљжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГПьВЭДњТєЕъДњЪлЖржжРраЭЕФПьВЭЃЌЩюЪмЙуДѓЯћЗбепЯВАЎ.ЦфжаЃЌ![]() жжРраЭЕФПьВЭУПЗнНјМлЮЊ
жжРраЭЕФПьВЭУПЗнНјМлЮЊ![]() дЊЃЌВЂвдУПЗн
дЊЃЌВЂвдУПЗн![]() дЊЕФМлИёЯњЪл.ШчЙћЕБЬь20:00жЎЧАТєВЛЭъЃЌЪЃгрЕФИУжжПьВЭУПЗнвд
дЊЕФМлИёЯњЪл.ШчЙћЕБЬь20:00жЎЧАТєВЛЭъЃЌЪЃгрЕФИУжжПьВЭУПЗнвд![]() дЊЕФМлИёзїЬиМлДІРэЃЌЧвШЋВПЪлЭъ.
дЊЕФМлИёзїЬиМлДІРэЃЌЧвШЋВПЪлЭъ.
ЃЈ1ЃЉШєИУДњТєЕъУПЬьЖЈжЦ![]() Зн
Зн![]() жжРраЭПьВЭЃЌЧѓ
жжРраЭПьВЭЃЌЧѓ![]() жжРраЭПьВЭЕБЬьЕФРћШѓ
жжРраЭПьВЭЕБЬьЕФРћШѓ![]() ЃЈЕЅЮЛЃКдЊЃЉЙигкЕБЬьашЧѓСП
ЃЈЕЅЮЛЃКдЊЃЉЙигкЕБЬьашЧѓСП![]() ЃЈЕЅЮЛЃКЗнЃЌ
ЃЈЕЅЮЛЃКЗнЃЌ![]() ЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИУДњТєЕъМЧТМСЫвЛИідТ![]() ЬьЕФ
ЬьЕФ![]() жжРраЭПьВЭШеашЧѓСПЃЈУПЬь20:00жЎЧАЯњЪлЪ§СПЃЉ
жжРраЭПьВЭШеашЧѓСПЃЈУПЬь20:00жЎЧАЯњЪлЪ§СПЃЉ
ШеашЧѓСП |
|
|
|
|
|
|
ЬьЪ§ |
|
|
|
|
|
|
ЃЈiЃЉМйЩшДњТєЕъдкетвЛИідТФкУПЬьЖЈжЦ![]() Зн
Зн![]() жжРраЭПьВЭЃЌЧѓетвЛИідТ
жжРраЭПьВЭЃЌЧѓетвЛИідТ![]() жжРраЭПьВЭЕФШеРћШѓЃЈЕЅЮЛЃКдЊЃЉЕФЦНОљЪ§ЃЈОЋШЗЕН
жжРраЭПьВЭЕФШеРћШѓЃЈЕЅЮЛЃКдЊЃЉЕФЦНОљЪ§ЃЈОЋШЗЕН![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈiiЃЉШєДњТєЕъУПЬьЖЈжЦ![]() Зн
Зн![]() жжРраЭПьВЭЃЌвд
жжРраЭПьВЭЃЌвд![]() ЬьМЧТМЕФШеашЧѓСПЕФЦЕТЪзїЮЊШеашЧѓСПЗЂЩњЕФИХТЪЃЌЧѓ
ЬьМЧТМЕФШеашЧѓСПЕФЦЕТЪзїЮЊШеашЧѓСПЗЂЩњЕФИХТЪЃЌЧѓ![]() жжРраЭПьВЭЕБЬьЕФРћШѓВЛЩйгк
жжРраЭПьВЭЕБЬьЕФРћШѓВЛЩйгк![]() дЊЕФИХТЪ.
дЊЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌжаУРУГвзФІВСВЛЖЯ.ЬиБ№ЪЧУРЙњЖдЮвЙњЛЊЮЊЕФЯожЦ.ОЁЙмУРЙњЖдЛЊЮЊМЋСІЗтЫјЃЌАйАуЕѓФбЃЌВЂВЛЖЯМгДѓЖдИїЙњЕФЪЉбЙЃЌРТЃЫћУЧЕжжЦЛЊЮЊ5GЃЌШЛЖјетВЂУЛгаШУЛЊЮЊШДВН.ЛЊЮЊдк2018ФъВЛНіОЛРћШѓДДЯТМЧТМЃЌКЃЭтдіГЄЭЌбљЧПОЂ.НёФъЃЌЮвЙњЛЊЮЊФГвЛЦѓвЕЮЊСЫНјвЛВНдіМгЪаГЁОКељСІЃЌМЦЛЎдк2020ФъРћгУаТММЪѕЩњВњФГПюаТЪжЛњ.ЭЈЙ§ЪаГЁЗжЮіЃЌЩњВњДЫПюЪжЛњШЋФъашЭЖШыЙЬЖЈГЩБО250ЭђЃЌУПЩњВњ![]() ЃЈЧЇВПЃЉЪжЛњЃЌашСэЭЖШыГЩБО
ЃЈЧЇВПЃЉЪжЛњЃЌашСэЭЖШыГЩБО![]() ЭђдЊЃЌЧв
ЭђдЊЃЌЧв 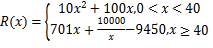 ЃЌгЩЪаГЁЕїбажЊЃЌУПВПЪжЛњЪлМл0.7ЭђдЊЃЌЧвШЋФъФкЩњВњЕФЪжЛњЕБФъФмШЋВПЯњЪлЭъ.
ЃЌгЩЪаГЁЕїбажЊЃЌУПВПЪжЛњЪлМл0.7ЭђдЊЃЌЧвШЋФъФкЩњВњЕФЪжЛњЕБФъФмШЋВПЯњЪлЭъ.
ЃЈ![]() ЃЉЧѓГі2020ФъЕФРћШѓ
ЃЉЧѓГі2020ФъЕФРћШѓ![]() ЃЈЭђдЊЃЉЙигкФъВњСП
ЃЈЭђдЊЃЉЙигкФъВњСП![]() ЃЈЧЇВПЃЉЕФКЏЪ§ЙиЯЕЪНЃЌЃЈРћШѓ=ЯњЪлЖюЁЊГЩБОЃЉЃЛ
ЃЈЧЇВПЃЉЕФКЏЪ§ЙиЯЕЪНЃЌЃЈРћШѓ=ЯњЪлЖюЁЊГЩБОЃЉЃЛ
![]() 2020ФъВњСПЮЊЖрЩйЃЈЧЇВПЃЉЪБЃЌЦѓвЕЫљЛёРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
2020ФъВњСПЮЊЖрЩйЃЈЧЇВПЃЉЪБЃЌЦѓвЕЫљЛёРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЮоТл![]() ШЁКЮжЕЃЌжБЯп
ШЁКЮжЕЃЌжБЯп![]() ЪМжеОЙ§ЕквЛЯѓЯоЃЛ
ЪМжеОЙ§ЕквЛЯѓЯоЃЛ
ЃЈ2ЃЉШєжБЯп![]() гы
гы![]() жсе§АыжсНЛгк
жсе§АыжсНЛгк![]() ЕуЃЌгы
ЕуЃЌгы![]() жсе§АыжсНЛгк
жсе§АыжсНЛгк![]() ЕуЃЌ
ЕуЃЌ![]() ЮЊзјБъдЕуЃЌЩш
ЮЊзјБъдЕуЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕМАДЫЪБжБЯп
ЕФзюаЁжЕМАДЫЪБжБЯп![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЕШ ВюЪ§Са
ЃЎЕШ ВюЪ§Са![]() жаЃЌ
жаЃЌ ![]() ЃЌЧвЙЋВю
ЃЌЧвЙЋВю![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉЪЧЗёДцдке§ећЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ?ЃЎШєДцдкЃЌЧѓГі
?ЃЎШєДцдкЃЌЧѓГі![]() ЕФзюаЁжЕЃЛШє ВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзюаЁжЕЃЛШє ВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() ЃК
ЃК ![]() ОЙ§ЭждВ
ОЙ§ЭждВ![]() ЃК
ЃК ![]() ЕФзѓгвНЙЕу
ЕФзѓгвНЙЕу![]() ЃЌЧвгыЭждВ
ЃЌЧвгыЭждВ![]() дкЕквЛЯѓЯоЕФНЛЕуЮЊ
дкЕквЛЯѓЯоЕФНЛЕуЮЊ![]() ЃЌЧв
ЃЌЧв![]() Ш§ЕуЙВЯпЃЌжБЯп
Ш§ЕуЙВЯпЃЌжБЯп![]() НЛЭждВ
НЛЭждВ![]() гк
гк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЈ
ЃЈ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЕБШ§НЧаЮ![]() ЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌЧѓжБЯп
ЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкRЩЯЕФКЏЪ§fЃЈxЃЉЃО0ЃЌЖдШЮвтxЃЌyЁЪRЖМгаfЃЈx+yЃЉЃНfЃЈxЃЉ fЃЈyЃЉГЩСЂЃЌЧвЕБxЃО0ЪБЃЌfЃЈxЃЉЃО1ЃЎ
ЃЈ1ЃЉЧѓfЃЈ0ЃЉЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄfЃЈxЃЉдкRЩЯЪЧдіКЏЪ§ЃЛ
ЃЈ3ЃЉШєfЃЈk3xЃЉfЃЈ3xЉ9xЉ2ЃЉЃМ1ЖдШЮвтxЁЪRКуГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() Й§Еу
Й§Еу![]() ЃЌЦфВЮЪ§ЗНГЬЮЊ
ЃЌЦфВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЌ
ЮЊВЮЪ§ЃЌ![]() ЃЉЃЌвд
ЃЉЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЧѓвбжЊЧњЯп![]() КЭЧњЯп
КЭЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com