|
|
|
要制作一个容积为4 m3,高为1 m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该溶器的最低总造价是
|
| [ ] |
A. |
80元
|
B. |
120元
|
C. |
160元
|
D. |
240元
|
|
|
答案:C
解析:
|
设池底长和宽分别为a,b,成本为y,则
∵长方形容器的容器为4 m3,高为1 m,
∴底面面积S=ab=4,y=20S+10[2(a+b)]=20(a+b)+80,
∵a+b≥2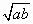 =4,∴当a=b=2时,y取最小值160, =4,∴当a=b=2时,y取最小值160,
即该容器的最低总造价是160元,故选:C.
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设a=sin33°,b=cos55°,c=tan35°,则
|
| [ ] |
A. |
a>b>c
|
B. |
b>c>a
|
C. |
c>b>a
|
D. |
c>a>b
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知集合M={-1,0,1},N={0,1,2},则M∪N=
|
| [ ] |
A. |
{-1,0,1}
|
B. |
{-1,0,1,2}
|
C. |
{-1,0,2}
|
D. |
{0,1}
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
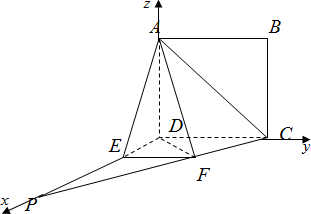
(1)证明:CF⊥平面ADF.
(2)求二面角D-AF-E的余弦值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
阅读下图所示的程序框图,运行相应的程序,输出的n的值为
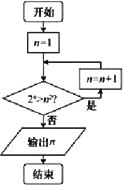
|
| [ ] |
A. |
1
|
B. |
2
|
C. |
3
|
D. |
4
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,A=60°,AC=2,BC= ,则AB等于________. ,则AB等于________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知曲线г上的点到点F(0,1)的距离比它到直线y=-3的距离小2.
(1)求曲线г的方程;
(2)曲线г在点P处的切线l与x轴交于点A.直线y=3分别与直线l及y轴交于点M,N,以MN为直径作圆C,过点A作圆C的切线,切点为B,试探究:当点P在曲线г上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=cosx(sinx+cosx)- . .
(1)若 ,且 ,且 ,求f(α)的值; ,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设函数f(x)=sin(ωx+φ),A>0,ω>0,若f(x)在区间 上具有单调性,且 上具有单调性,且 ,则f(x)的最小正周期为________. ,则f(x)的最小正周期为________.
|
|
|
查看答案和解析>>
