
【题目】对哪些正整数n,存在正整数 m 及正整数![]() ,使得
,使得![]() ?其中
?其中![]() 可以相同,且
可以相同,且![]() .
.
【答案】见解析
【解析】
先设 n ≥12 且n不满足要求.设 m为偶数,
![]() .
.
则![]() ,且
,且
![]() .
.
设 l为最小的正整数, 使得![]() .令
.令![]() ,其中,t、s为非负整数,
,其中,t、s为非负整数,![]() .
.
由于n不满足要求 ,故 r 不可表示为不超过 2l -1个平方和, 且其中每一个不超过![]() .从而,s不可表为不超过
.从而,s不可表为不超过![]() 个平方和.
个平方和.
当 l≥6 时,由![]() ,知
,知![]() .因此,t ≤6.
.因此,t ≤6.
设![]() 为非负整数,
为非负整数,![]() .
.
由![]() ,知
,知![]() .
.
从而,![]() .
.
若![]() ,则s可表为不超过4个平方和,
,则s可表为不超过4个平方和,![]() ,矛盾;
,矛盾;
若![]() ,则s可给为不超过5个平方和,
,则s可给为不超过5个平方和,![]() ,矛盾;
,矛盾;
若![]() ,则
,则![]() ,s可给为不超过
,s可给为不超过![]() 个平方和,矛盾.
个平方和,矛盾.
因此,l≤5 .
当l=5 时 ,
![]() .
.
设![]() .则
.则![]() .
.
若 t = 7 ,则由 r ≤112 知 s =0 ,此时,r 可表为7个42之和, 矛盾 ;
若 t = 6 ,验证知当 0 ≤s ≤15 , s ≠7,15时,s可表为 3个平方和,又
![]() ,
,
![]() ,矛盾.
,矛盾.
当 l =4 时, 2l-1 =7,
![]() .
.
若 t ≤4,s ≠7,
则由 s 可表为不超过 3个平方和, 3 ≤2l -1 -t ,矛盾;
若 1 ≤t ≤4,s =7 ,
则![]() ,矛盾;
,矛盾;
若 t = 0 , s = 7 ,
则 r 可表为 7个12之和,矛盾 .
因此 , t ≥5.
从而,![]() ,
,
![]() .
.
当l ≤3 时,![]() .
.
下面只要考虑 n ≤67.
由于![]() , 故只要考虑 m ≤9 .
, 故只要考虑 m ≤9 .
表1
m | a(m - a)可能取值 | m - 1个形如 a(m - a)之和且小于或等于 67 |
9 | 8,14,18,20 | 64 |
8 | 7,12,15,16 | 49,54,57,58,59,62,63,64,65,66,67 |
7 | 6,10,12 | 36,40,42,44,46,48,50,52,54,56,58,60,62,64,66 |
6 | 5,8,9 | 25,28,29,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45 |
5 | 4,6 | 16,18,20,22,24 |
4 | 3,4 | 9,10,11,12 |
3 | 2 | 4 |
2 | 1 | 1 |
查表 1知不满足要求的 n 为:2 , 3 , 5 , 6 ,7 , 8 , 13 , 14 , 15 , 17 , 19 , 21 , 23 , 26 , 27 , 30 , 47 , 51 ,53 , 55 , 61 ,其余 n 均满足要求.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,侧面ABE⊥底面BCDE,BC=2,CD=4。
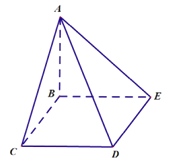
(I)证明:AB⊥面BCDE;
(II)若AD=2![]() ,求二面角C-AD-E的正弦值。
,求二面角C-AD-E的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均为2,
的各棱长均为2, ![]() 面
面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)求证:直线BE∥平面![]() ;
;
(2)平面![]() 与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥
与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某市2011年新建住房400万m2,其中250万m2是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积比上一年增加50万m2,那么到哪一年底,
(1)该市历年所建中低价房的累计面积(以2011年为累计的第一年)将首次不少于4750万m2?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)若点![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,点
的左右顶点,点![]() 是椭圆
是椭圆![]() 上不同于
上不同于![]() 的动点,直线
的动点,直线![]() 与
与![]() 直线x=a交于点
直线x=a交于点![]() ,证明:以线段
,证明:以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线C上的一点,线段PF1与y轴的交点M恰好是线段PF1的中点,
(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线C上的一点,线段PF1与y轴的交点M恰好是线段PF1的中点,![]() ,其中O为坐标原点,则双曲线C的渐近线的斜率与离心率分别是( )
,其中O为坐标原点,则双曲线C的渐近线的斜率与离心率分别是( )
A. ±1,![]() B. 1,
B. 1,![]() C. ±2,
C. ±2,![]() D. 2,
D. 2,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为![]() 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)求曲线C的极坐标方程;
(2)设直线l的极坐标方程为![]() ,若直线l与曲线C交于M,N两点,且
,若直线l与曲线C交于M,N两点,且![]() ,求直线l的直角坐标方程.
,求直线l的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com