练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,求动圆圆心M的轨迹方程.

    解:如图,设动圆M与圆C1及圆C2分别外切于点A和B,根据两圆外切的充要条件,得|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|.

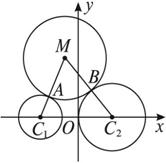
    ∵|MA|=|MB|,∴|MC1|-|AC1|=|MC2|-|BC2|.

    ∴|MC2|-|MC1|=|BC2|-|AC1|=3-1=2.

        这表明动点M与两定点C2、C1的距离的差是常数2.根据双曲线的定义,动点M的轨迹为双曲线的左支(点M与C2的距离大,与C1的距离小).

        这里a=1,c=3,则b2=8,设点M的坐标为(x,y),则其轨迹方程为x2=1(x＜0).

    点评:由于动点M到两定点C2、C1的距离的差为常数,而不是差的绝对值为常数,因此,其轨迹只能是双曲线的一支,这一点要特别注意!

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在平面直角坐标系xoy中，已知圆C1：（x+3）2+y2=4．若直线l过点A（4，-1），且被圆C1截得的弦长为2
    		3
    ，求直线l的方程；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C1(x+2)2+(y-1)2=1，圆C2(x-3)2+(y-4)2=9，M，N分别是圆C1，
    C
     
    2
    上的动点，P为x轴上的动点，则|PM|+|PN|的最小值为（　　）

    查看答案和解析>>

    科目：高中数学 来源：高考总复习全解　数学　一轮复习·必修课程　（人教实验版）　B版 人教实验版　B版 题型：044

    已知圆C1∶(x＋1)2＋(y－3)2＝9，圆C2∶x2＋y2－4x＋2y－11＝0，求两圆公共弦所在直线的方程及公共弦的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C1:(x+1)2+(y-3)2=25,圆C2与圆C1关于点(2,1)对称,则圆C2的方程是(    )

    A.(x-3)2+(y-5)2=25

    B.(x-5)2+(y+1)2=25

    C.(x-1)2+(y-4)2=25

    D.(x-3)2+(y+2)2=25

    查看答案和解析>>

    同步练习册答案