
【题目】已知函数f(x)=﹣x2+2|x﹣a|,x∈R.
(1)若函数f(x)为偶函数,求实数a的值;
(2)当x=﹣1时,函数f(x)在x=﹣1取得最大值,求实数a的取值范围.
(3)若函数f(x)有三个零点,求实数a的取值范围.
【答案】
(1)解:任取x∈R,则f(﹣x)=f(x)恒成立,
即﹣(﹣x)2+2|﹣x﹣a|=﹣x2+2|x﹣a|恒成立,
∴|x﹣a|=|x+a|恒成立,
两边平方得:x2﹣2ax+a2=x2+2ax+a2,
∴a=0;
(2)解: 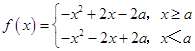 ,因为函数y=f(x)在x=﹣1时取得最大值,
,因为函数y=f(x)在x=﹣1时取得最大值,
当a≥1时,必须f(﹣1)≥f(a),即1+2a≥﹣a2+2a﹣2a,即(a+1)2≥0,所以a≥1适合题意;
当﹣1<a<1时,必须f(﹣1)≥f(1),即1+2a≥1﹣2a,即a≥0,所以0≤a<1适合题意;
当a≤﹣1时,因为f(﹣1)<f(1),不合题意,
综上,实数a的取值范围是[0,+∞).
(3)解: 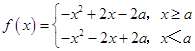 ,
,
![]() ,
, ![]() ,
,
当△1=0时, ![]() ,此时函数
,此时函数 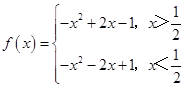 有三个零点1,
有三个零点1, ![]() ;
;
当△2=0时, ![]() ,此时函数
,此时函数 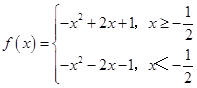 有三个零点
有三个零点 ![]() ;
;
当△1>0,△2>0时,即 ![]() 时,方程﹣x2+2x﹣2a=0的两根为
时,方程﹣x2+2x﹣2a=0的两根为 ![]() ,
,
方程﹣x2﹣2x+2a=0的两根为 ![]() ,
,
因为 ![]() ,所以
,所以 ![]() 且
且 ![]() ,解得a=0,
,解得a=0,
或者 ![]() 且
且 ![]() ,此时无解,
,此时无解,
综上得 ![]() 或0.
或0.
【解析】(1)由偶函数的定义,可得f(﹣x)=f(x),化简整理可得a=0;(2)去绝对值,运用分段函数的形式,写出f(x),讨论当a≥1时,当﹣1<a<1时,当a≤﹣1时,考虑最大值,解不等式即可得到a的范围;(3)去绝对值,运用分段函数的形式,写出f(x),讨论两个二次函数的判别式,等于0或大于0,解方程(或不等式)即可得到a的值.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知点G(5,4),圆C1:(x﹣1)2+(y﹣4)2=25,过点G的动直线l与圆C1 , 相交于两点E、F,线段EF的中点为C. (Ⅰ)求点C的轨迹C2的方程;
(Ⅱ)若过点A(1,0)的直线l1:kx﹣y﹣k=0,与C2相交于两点P、Q,线段PQ的中点为M,l1与l2:x+2y+2=0的交点为N,求证:|AM||AN|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为四棱锥P﹣ABCD的表面展开图,四边形ABCD为矩形, ![]() ,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为
,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为 ![]() ,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 .
,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 . 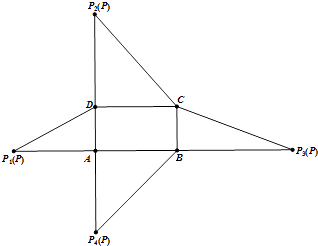
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点. 
(1)求证:MN∥BC;
(2)若M,N分别为PB,PC的中点,
①求证:PB⊥DN;
②求二面角P﹣DN﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中,AA1=2,BC= ![]() ,E为CC1的中点.
,E为CC1的中点. 
(1)求证:平面A1BE⊥平面B1CD;
(2)平面A1BE与底面A1B1C1D1所成的锐二面角的大小为θ,当 ![]() 时,求θ的取值范围.
时,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= ![]() ,AB=AC.
,AB=AC. 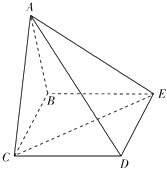
(1)证明:AD⊥CE;
(2)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线l:y=kx﹣2.
(1)若直线l与圆O交于不同的两点A,B,当 ![]() 时,求k的值;
时,求k的值;
(2)若 ![]() 是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若EF、GH为圆O:x2+y2=2的两条相互垂直的弦,垂足为 ![]() ,求四边形EGFH的面积的最大值.
,求四边形EGFH的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= ![]() )
)
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com