
【题目】P(x0 , y0)(x0≠±a)是双曲线E: ![]() 上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为
上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为 ![]() .
.
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足 ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:∵P(x0,y0)(x0≠±a)是双曲线E: ![]() 上一点,
上一点,
∴ ![]() ,①
,①
由题意又有 ![]() ,②
,②
联立①、②可得a2=5b2,c2=a2+b2,
则e= ![]() ,
,
(2)联立 ![]() ,得4x2﹣10cx+35b2=0,
,得4x2﹣10cx+35b2=0,
设A(x1,y1),B(x2,y2),
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
设 ![]() =(x3,y3),
=(x3,y3), ![]() ,
,
即 ![]()
又C为双曲线上一点,即x32﹣5y32=5b2,
有(λx1+x2)2﹣5(λy1+y2)2=5b2,
化简得:λ2(x12﹣5y12)+(x22﹣5y22)+2λ(x1x2﹣5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在双曲线上,所以x12﹣5y12=5b2,x22﹣5y22=5b2,
而x1x2﹣5y1y2=x1x2﹣5(x1﹣c)(x2﹣c)
=﹣4x1x2+5c(x1+x2)﹣5c2=﹣4 ![]() +5c
+5c ![]() ﹣5c2=
﹣5c2= ![]() ﹣35b2=
﹣35b2= ![]() 6b2﹣35b2=10b2,
6b2﹣35b2=10b2,
得λ2+4λ=0,解得λ=0或﹣4.
【解析】(1)由P点坐标满足双曲线方程,直线PM,PN的斜率之积为 ![]() 联立方程组可得a2=5b2,即可求出e的值。
联立方程组可得a2=5b2,即可求出e的值。
(2)可求出过双曲线E的右焦点且斜率为1的直线y=x-c,与双曲线联立方程组求出x1+x2,x1x2。由 ![]() 可求出
可求出![]() 值。
值。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆 ![]() =1(a>b>0),F1 , F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1 , F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.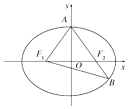
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若椭圆的焦距为2,且 ![]() =2
=2 ![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:其中正确命题的序号是 .
①设a,b是非零实数,若a<b,则ab2<a2b;
②若a<b<0,则 ![]() >
> ![]() ;
;
③函数y= ![]() 的最小值是2;
的最小值是2;
④若x,y是正数, ![]() +
+ ![]() =1,则x+2y的最小值为8.
=1,则x+2y的最小值为8.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的个数是( )
①若正实数![]() 满足
满足![]() ,则
,则![]() 的最小值是16;
的最小值是16;
②已知![]() ,则函数
,则函数![]() 的最大值为
的最大值为![]() ;
;
③已知![]() ,且
,且![]() ,则
,则![]() 的最小值是36;
的最小值是36;
④若对任意实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() 。
。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com