过点(-1,1)且与圆x2+y2-4x+2y-4=0相切的直线的方程为( )
A.5x-12y+17=0
B.5x-12y+17=0或5x+12y+17=0
C.x=-1或5x+12y+17=0
D.x=-1或5x-12y+17=0
【答案】
分析:先考虑过点(-1,1)的直线斜率不存在时是否与圆相切,再考虑过点(-1,1)的直线斜率存在时,设出直线的斜率,利用直线与圆的相切的几何性质:圆心到直线的距离等于半径,即可解得直线斜率,进而得直线方程
解答:解:圆x
2+y
2-4x+2y-4=0即(x-2)
2+(y+1)
2=9
当过点(-1,1)的直线斜率不存在时,即x=-1,圆心(2,-1)到此直线的距离为2-(-1)=3,等于半径
∴直线x=-1符合题意,
当过点(-1,1)的直线斜率存在时,设直线方程为y-1=k(x+1),即kx-y+k+1=0
∵过点(-1,1)且与圆x
2+y
2-4x+2y-4=0相切
∴圆心(2,-1)到直线的距离等于半径3,即
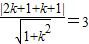
解得:k=
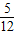
,此时直线方程为5x-12y+17=0
综上所述,过点(-1,1)且与圆x
2+y
2-4x+2y-4=0相切的直线的方程为x=-1或5x-12y+17=0
故选 D
点评:本题考查了直线与圆的位置关系,待定系数法求直线方程的技巧,点到直线的距离公式,分类讨论的思想方法

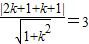
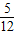 ,此时直线方程为5x-12y+17=0
,此时直线方程为5x-12y+17=0
