Question

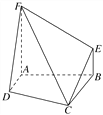
【题目】如图，四边形ABEF和四边形ABCD均是直角梯形，∠FAB＝∠DAB＝90°，二面角FABD是直二面角，BE∥AF，BC∥AD，AF＝AB＝BC＝2，AD＝1.

(1)证明：在平面BCE上，一定存在过点C的直线l与直线DF平行；

(2)求二面角FCDA的余弦值．

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）推导出平面BCE∥平面ADF．设平面DFC∩平面BCE=l，则l过点C．由平面BCE∥平面ADF，平面DFC∩平面BCE=l，得到DF∥l，由此能证明在平面BCE上一定存在过点C的直线l，使得DF∥l．（2）以A为原点，AD，AB，AF分别为x轴，y轴，z轴建立空间直角坐标系，利用向量法能求出二面角FCDA的余弦值．

试题解析：

(1)证明：由已知得，BE∥AF，BE平面AFD，AF平面AFD，

∴BE∥平面AFD.

同理可得，BC∥平面AFD.

又BE∩BC＝B，∴平面BCE∥平面AFD.

设平面DFC∩平面BCE＝l，则l过点C.

∵平面BCE∥平面ADF，平面DFC∩平面BCE＝l，平面DFC∩平面AFD＝DF，

∴DF∥l，即在平面BCE上一定存在过点C的直线l，使得DF∥l.

(2)∵平面ABEF⊥平面ABCD，平面ABCD∩平面ABEF＝AB，FA平面ABEF，

又∠FAB＝90°，∴AF⊥AB，∴AF⊥平面ABCD.

∵AD平面ABCD，∴AF⊥AD.

∵∠DAB＝90°，∴AD⊥AB.

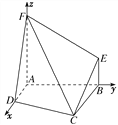
以A为坐标原点，AD，AB，AF所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，由已知得，D(1,0,0)，C(2，2,0)，F(0,0,2)，∴＝(－1,0,2)，＝(1,2,0)．

设平面DFC的法向量为n＝(x，y，z)，

则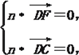即

令z＝1，则n＝(2，－1,1)，

不妨取平面ACD的一个法向量为m＝(0,0,1)，

∴cos〈m，n〉＝＝＝，

由于二面角FCDA为锐角，

因此二面角FCDA的余弦值为.