
【题目】已知圆![]() ,点
,点![]() 是直线l:
是直线l:![]() 上的动点,若在圆C上总存在不同的两点A,B使得
上的动点,若在圆C上总存在不同的两点A,B使得![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
【答案】![]()
【解析】
由在圆![]() 上总存在不同的两点A,B使得
上总存在不同的两点A,B使得![]() 可知四边形OAPB是菱形,于是
可知四边形OAPB是菱形,于是![]() 垂直平分
垂直平分![]() .然后分类讨论:当直线
.然后分类讨论:当直线![]() 的斜率为0时,此时在圆
的斜率为0时,此时在圆![]() 上不存在不同的两点
上不存在不同的两点![]() 满足条件.当直线
满足条件.当直线![]() 的斜率不存在时,可得
的斜率不存在时,可得![]() ,此时直线
,此时直线![]() 方程为为
方程为为![]() ,满足条件.当直线
,满足条件.当直线![]() 的斜率存在且不为0时,利用
的斜率存在且不为0时,利用![]() ,
,![]() ,可得直线
,可得直线![]() 方程为
方程为![]() ,圆心到直线
,圆心到直线![]() 的距离
的距离![]() ,即
,即![]() ,再利用
,再利用![]() ,即可解出所求范围.
,即可解出所求范围.
∵在圆![]() 上总存在不同的两点
上总存在不同的两点![]() 使得
使得![]() ,
,
∴四边形OAPB是菱形,
∴直线![]() 垂直平分OP.
垂直平分OP.
①当直线![]() 的斜率为0时,由直线
的斜率为0时,由直线![]() 得
得![]() ,此时在圆
,此时在圆![]() 上不存在不同的两点
上不存在不同的两点![]() 满足条件.
满足条件.
②当直线![]() 的斜率不存在时,由直线
的斜率不存在时,由直线![]() 可得
可得![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() ,满足条件.
,满足条件.
③当直线![]() 的斜率存在且不为0时,
的斜率存在且不为0时,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由题意得圆心到直线![]() 的距离
的距离![]() ,即
,即![]() ,
,
又![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
①对于任意一个圆O,其“优美函数”有无数个;
②函数f(x)=ln(![]() )可以是某个圆的“优美函数”;
)可以是某个圆的“优美函数”;
③函数y=1+sinx可以同时是无数个圆的“优美函数”;
④函数y=2x+1可以同时是无数个圆的“优美函数”;
⑤函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的命题是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的焦距为
.已知椭圆的焦距为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() (
(![]() )与椭圆交于
)与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
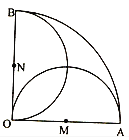
【题目】如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的一个焦点是
的一个焦点是![]() ,且
,且![]()
(1)求双曲线![]() 的方程
的方程
(2)设经过焦点![]() 的直线
的直线![]() 的一个法向量为
的一个法向量为![]() ,当直线
,当直线![]() 与双曲线
与双曲线![]() 的右支相交于不同的两点
的右支相交于不同的两点![]() 时,求实数
时,求实数![]() 的取值范围
的取值范围
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 的右支相交于
的右支相交于![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得
,使得![]() 为锐角?若存在,请求出
为锐角?若存在,请求出![]() 的范围;若不存在,请说明理由
的范围;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
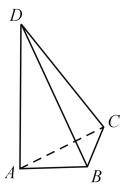
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
①相关系数![]() 用来衡量两个变量之间线性关系的强弱,
用来衡量两个变量之间线性关系的强弱,![]() 越接近于1,相关性越弱;
越接近于1,相关性越弱;
②回归直线![]() 过样本点中心
过样本点中心![]() ;
;
③相关指数![]() 用来刻画回归的效果,
用来刻画回归的效果,![]() 越小,说明模型的拟合效果越不好.
越小,说明模型的拟合效果越不好.
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
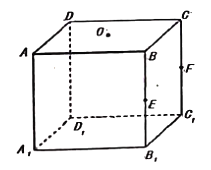
【题目】如下图,在正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,点
的中点,点![]() 为上底面的中心,过
为上底面的中心,过![]() 三点的平面把正方体分为两部分,其中含
三点的平面把正方体分为两部分,其中含![]() 的部分为
的部分为![]() ,不含
,不含![]() 的部分为
的部分为![]() ,连接
,连接![]() 和
和![]() 的任一点
的任一点![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com