
【题目】如图,已知AB是圆O的直径,C是圆O上一点,AC=BC,且PA⊥平面ABC,E是AC的中点,F是PB的中点,PA=![]() ,AB=2.求:
,AB=2.求:
(Ⅰ)异面直线EF与BC所成的角;
(Ⅱ)点A到平面PBC的距离.

【答案】(Ⅰ)60°(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接OE,OF,说明∠FEO是异面直线EF与BC所成的角,解三角形![]() 即可。
即可。
(Ⅱ)证明BC⊥平面PAC,即可计算出S△PBC=2,利用等体积法列方程即可得解。
解:(I)连接OE,OF.

∵O是AB的中点,E是AC的中点,
∴OE∥BC,
∴∠FEO是异面直线EF与BC所成的角,
∵O是AB的中点,F是PB的中点,
∴OF∥PA,又PA⊥平面ABC,
∴OF⊥平面ABC,
∵AB是圆O的直径,∴AC⊥BC,
∵AC=BC,AB=2,∴BC=![]() ,∴OE=
,∴OE=![]() BC=
BC=![]() ,
,
又OF=![]() PA=
PA=![]() ,∴tan∠FEO=
,∴tan∠FEO=![]() =
=![]() ,
,
∴异面直线EF与BC所成的角为60°.
(II)∵PA⊥平面ABC,BC平面ABC,
∴PA⊥BC,
∵AB是圆O的直径,∴AC⊥BC,
又PA∩AC=A,
∴BC⊥平面PAC,∴BC⊥PC.
∵PC=![]() =2
=2![]() ,∴S△PBC=
,∴S△PBC=![]() =2.
=2.
设A到平面PBC的距离为h,则VA-PBC=![]() =
=![]() .
.
又VA-PBC=VP-ABC=![]() =
=![]() =
=![]() ,
,
∴h=![]() ,即A到平面PBC的距离为
,即A到平面PBC的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.互相垂直的两条直线的直观图仍然是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() :
:![]() .
.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知![]() ,圆
,圆![]() 与x轴相交于两点
与x轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
:![]() 相交于两点A,B.问:是否存在实数a,使得
相交于两点A,B.问:是否存在实数a,使得![]() =
=![]() ?若存在,求出实数a的值,若不存在,请说明理由.
?若存在,求出实数a的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l方程为(m+2)x-(m+1)y-3m-7=0,m∈R.
(Ⅰ)求证:直线l恒过定点P,并求出定点P的坐标;
(Ⅱ)若直线l在x轴,y轴上的截距相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E,F,G分别在棱SA,SB,SC上,且平面EFG∥平面ABC,点E为SA的中点.求证:
(Ⅰ)AF⊥平面SBC;
(Ⅱ)SA⊥BC.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 若该大学某女生身高为170cm,则可断定其体重必为![]()
B. 回归直线过样本点的中心![]()
C. 若该大学某女生身高增加1cm,则其体重约增加![]()
D. y与x具有正的线性相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
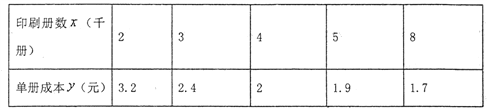
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
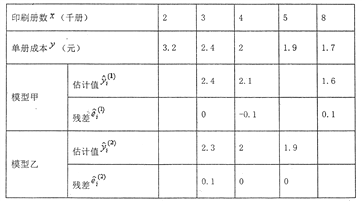
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,求印刷厂二次印刷10千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”,共有4个选项:A,1.5小时以上,B,1-1.5小时,C,0.5-1小时,D,0.5小时以下.图(1),(2)是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
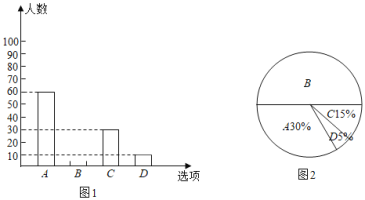
(1)本次一共调查了多少名学生.
(2)在图(1)中将![]() 对应的部分补充完整.
对应的部分补充完整.
(3)若该校有3000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com