
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到![]() 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为![]() ;当车流密度不超过
;当车流密度不超过![]() 辆/千米时,车流速度为
辆/千米时,车流速度为![]() 千米/小时,研究表明:当
千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
科目:高中数学 来源: 题型:
【题目】(1)已知a,b,N都是正数,a≠1,b≠1,证明对数换底公式:logaN=![]() ;
;
(2)写出对数换底公式的一个性质(不用证明),并举例应用这个性质.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|-1,(a为常数).
(1)若f(x)在x∈[0,2]上的最大值为3,求实数a的值;
(2)已知g(x)=xf(x)+a-m,若存在实数a∈(-1,2],使得函数g(x)有三个零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
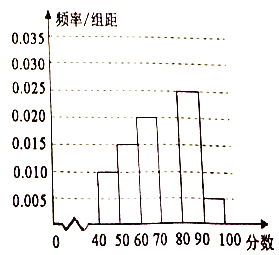
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市公司股票在30天内每股的交易价格P(元)关于时间t(天)的函数关系为 ,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点
,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点![]() 和点
和点![]() .
.
(1)求出日交易量Q(万股)与时间t(天)的一次函数关系式;
(2)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com