
分析 (1)设相应的获利为z,列出可行域,目标函数,分别求出目标函数的最大获利即可.
(Ⅱ)(Ⅱ)为使z当且仅当x=20,y=30时取最大值,则直线z=3ax+4by的斜率-$\frac{3a}{4b}$满足-$\frac{12}{8}<-\frac{3a}{4b}<-1$所以$\frac{4}{3}<\frac{a}{b}<2,\frac{8}{9}<\frac{1+4λ}{1+5λ-5{λ}^{2}}<\frac{4}{3}$,$\left\{\begin{array}{l}{40{λ}^{2}-4λ+1>0}\\{20{λ}^{2}-8λ-1<0}\end{array}\right.$⇒$\left\{\begin{array}{l}{x∈R}\\{-\frac{1}{10}<λ<\frac{1}{2}}\end{array}\right.$即可
解答  解:设工厂每天的获利为z元,由已知得z=3ax+4by,且
解:设工厂每天的获利为z元,由已知得z=3ax+4by,且
$\left\{\begin{array}{l}{12x+8y≤480}\\{x+y≤50}\\{3x≤102}\\{x≥0,y≥0}\end{array}\right.$,作出可行域如图所示.
(1)z=3ax+4by=72x+64y,当)z=72x+64y对应直线过点(20,30)时,z取最大值3360.
(Ⅱ)为使z当且仅当x=20,y=30时取最大值,则直线z=3ax+4by的斜率-$\frac{3a}{4b}$满足-$\frac{12}{8}<-\frac{3a}{4b}<-1$
所以$\frac{4}{3}<\frac{a}{b}<2,\frac{8}{9}<\frac{1+4λ}{1+5λ-5{λ}^{2}}<\frac{4}{3}$,
∴$\left\{\begin{array}{l}{40{λ}^{2}-4λ+1>0}\\{20{λ}^{2}-8λ-1<0}\end{array}\right.$
⇒$\left\{\begin{array}{l}{x∈R}\\{-\frac{1}{10}<λ<\frac{1}{2}}\end{array}\right.$,又因为0<λ<1∴0<λ<$\frac{1}{2}$
故λ的取值范围为(0,$\frac{1}{2}$)
点评 本题考查了线性规划的应用,考查分析问题解决问题的能力,属于基础题..


科目:高中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y3<y1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
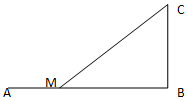 如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为50,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (-∞,-1) | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com