
| A. | 0.25 | B. | 0.30 | C. | 0.35 | D. | 0.40 |
分析 分别设出各个事件,得到P(C)=$\frac{P(\overline{A}B)}{P(\overline{A})}$=$\frac{P(B)-P(AB)}{1-P(A)}$,分别将P(A),P(B)代入求出P(C)即可.
解答 解:设“在30年内发生特大洪水”为事件A,
“在40年内发生特大洪水”为事件B,
“在未来10年内该地区将发生特大洪水”为事件C,
∴在未来10年内该地区将发生特大洪水的概率:
P(C)=$\frac{P(\overline{A}B)}{P(\overline{A})}$=$\frac{P(B)-P(AB)}{1-P(A)}$=$\frac{P(B)-P(A)}{1-P(A)}$=$\frac{0.85-0.8}{1-0.8}$=0.25,
故选:A.
点评 本题考查了相互独立事件,相互独立事件表示的是几个概率同时发不发生互不影响,比方说明天下不下雨和明天底部地震没有关系,他们发不发生互不影响.满足这种条件的事件就叫做相互独立事件.A、B个两个独立概率事件同时发生的概率为:P(A•B)=P(A)•P(B).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥S-ABCD是底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS的中点.
如图所示,四棱锥S-ABCD是底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
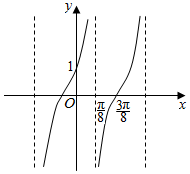
| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com