
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
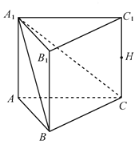
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)在棱
;(Ⅲ)在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
【解析】
(Ⅰ)可证明![]() 平面
平面![]() ,从而得到
,从而得到![]() .
.
(Ⅱ)利用![]() ,
,![]() ,
,![]() 两两互相垂直建立如图所示空间直角坐标系
两两互相垂直建立如图所示空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量平面
的法向量平面![]() 的法向量后可求二面角的余弦值.
的法向量后可求二面角的余弦值.
(Ⅲ)设![]() ,则可用
,则可用![]() 表示
表示![]() ,利用
,利用![]() 与平面
与平面![]() 的法向量垂直可求
的法向量垂直可求![]() ,从而得到
,从而得到![]() 的值.
的值.
证明:(Ⅰ)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
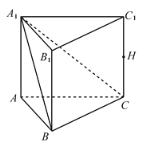
因为![]() ,所以
,所以![]() .
.
又因为![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
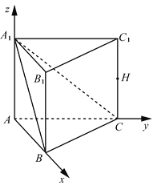
(Ⅱ)由(Ⅰ)可知![]() ,
,![]() ,
,![]() 两两互相垂直,
两两互相垂直,
如图,建立空间直角坐标系![]() .
.
因为![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 即为平面
即为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
则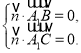 即
即![]()
令![]() ,则
,则![]() .
.
于是![]() .
.
所以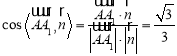 .
.
由题知二面角![]() 为锐角,所以其余弦值为
为锐角,所以其余弦值为![]() .
.
(Ⅲ)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() .
.
由![]() ,
,![]() 得
得![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
所以![]() .
.
若![]() 平面
平面![]() ,则
,则![]() ,解得
,解得![]() .
.
又因为![]() 平面
平面![]() .
.
所以在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
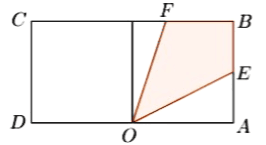
【题目】如图一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若探照灯每9分钟旋转“一个来回”(![]() 自
自![]() 转到
转到![]() ,再回到
,再回到![]() ,称“一个来回”,忽略
,称“一个来回”,忽略![]() 在
在![]() 及
及![]() 处所用的时间),且转动的角速度大小一定,设
处所用的时间),且转动的角速度大小一定,设![]() 边上有一点
边上有一点![]() ,且
,且![]() ,求点
,求点![]() 在“一个来回”中被照到的时间.
在“一个来回”中被照到的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点和上顶点分别为
的焦点和上顶点分别为![]() ,定义:
,定义:![]() 为椭圆
为椭圆![]() 的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点
的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点![]() 是椭圆
是椭圆![]() 的一个焦点,且
的一个焦点,且![]() 上任意一点到它的两焦点的距离之和为4
上任意一点到它的两焦点的距离之和为4
(1)若椭圆![]() 与椭圆
与椭圆![]() 相似,且
相似,且![]() 与
与![]() 的相似比为2:1,求椭圆
的相似比为2:1,求椭圆![]() 的方程.
的方程.
(2)已知点![]() 是椭圆
是椭圆![]() 上的任意一点,若点
上的任意一点,若点![]() 是直线
是直线![]() 与抛物线
与抛物线![]() 异于原点的交点,证明:点
异于原点的交点,证明:点![]() 一定在双曲线
一定在双曲线![]() 上.
上.
(3)已知直线![]() ,与椭圆
,与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆为
的椭圆为![]() ,是否存在正方形
,是否存在正方形![]() ,(设其面积为
,(设其面积为![]() ),使得
),使得![]() 在直线
在直线![]() 上,
上,![]() 在曲线
在曲线![]() 上?若存在,求出函数
上?若存在,求出函数![]() 的解析式及定义域;若不存在,请说明理由.
的解析式及定义域;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
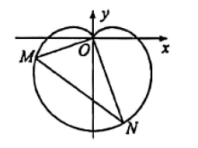
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com