
【题目】如图,椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,长轴是圆
,长轴是圆![]() :
:![]() 的直径.点
的直径.点![]() 是椭圆
是椭圆![]() 的下顶点,
的下顶点,![]() ,
,![]() 是过点
是过点![]() 且互相垂直的两条直线,
且互相垂直的两条直线,![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 的面积取最大值时,求直线
的面积取最大值时,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】在四面体SABC中若三条侧棱SA,SB,SC两两互相垂直,且SA=1,SB=![]() ,SC=
,SC=![]() ,则四面体ABCD的外接球的表面积为( )
,则四面体ABCD的外接球的表面积为( )
A.8πB.6πC.4πD.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE及平面DEC都与平面ADE垂直.

(1)求证:BC∥平面ADE;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将4本不同的书随机放入如图所示的编号为1,2,3,4的四个抽屉中.
1 | 2 | 3 | 4 |
(Ⅰ)求4本书恰好放在四个不同抽屉中的概率;
(Ⅱ)随机变量![]() 表示放在2号抽屉中书的本数,求
表示放在2号抽屉中书的本数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点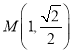 ,
,![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,与圆
两点,与圆![]() 相切与点
相切与点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)以线段![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,若点
,若点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() (
(![]() 是坐标原点),求实数
是坐标原点),求实数![]() 的取值范围;
的取值范围;
(3)![]() 是否为定值,如果是,求
是否为定值,如果是,求![]() 的值;如果不是,求
的值;如果不是,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国多地区遭遇了雾霾天气,引起口罩热销.某品牌口罩原来每只成本为6元.售价为8元,月销售5万只.
(1)据市场调查,若售价每提高0.5元,月销售量将相应减少0.2万只,要使月总利润不低于原来的月总利润(月总利润![]() 月销售总收入
月销售总收入![]() 月总成本),该口罩每只售价最多为多少元?
月总成本),该口罩每只售价最多为多少元?
(2)为提高月总利润,厂家决定下月进行营销策略改革,计划每只售价![]() 元,并投入
元,并投入![]() 万元作为营销策略改革费用.据市场调查,每只售价每提高0.5元,月销售量将相应减少
万元作为营销策略改革费用.据市场调查,每只售价每提高0.5元,月销售量将相应减少![]() 万只.则当每只售价
万只.则当每只售价![]() 为多少时,下月的月总利润最大?并求出下月最大总利润.
为多少时,下月的月总利润最大?并求出下月最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com