
| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
分析 根据函数的部分图象知ω=1,写出f(x)的解析式,再对选项中的命题进行分析、判断正误.
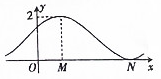
解答 解:根据函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象知,
ω=1,∴f(x)=sin(x+$\frac{π}{6}$)+1;
∴|MN|=$\frac{1}{2}$T=π,A正确;
f($\frac{7π}{3}$)=sin($\frac{7π}{3}$+$\frac{π}{6}$)+1=2,B正确;
f(x)+f(-x-$\frac{π}{3}$)=sin(x+$\frac{π}{6}$)+1+sin(-x-$\frac{π}{3}$+$\frac{π}{6}$)+1
=sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$-sinxcos$\frac{π}{3}$-cosxsin$\frac{π}{3}$+2
=$\frac{\sqrt{3}-1}{2}$(sinx-cosx)+2≠1,C错误;
x=$\frac{π}{3}$是f(x)=sin(x+$\frac{π}{6}$)图象的一条对称轴,
∴f($\frac{π}{3}$-x)=f($\frac{π}{3}$+x),D正确.
故选:C.
点评 本题考查了正弦函数的图象与性质的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (2,$\frac{33}{8}$) | C. | (2,$\frac{19}{8}$) | D. | ($\frac{19}{8}$,$\frac{33}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com