设
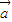
、
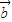
、
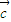
是三个非零向量,且

、
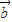
不共线,若关于x的方程
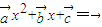
的两个根为x
1,x
2,则( )
A.x
1>x
2B.x
1=x
2C.x
1<x
2D.x
1,x
2大小无法确定
【答案】
分析:由题意可得
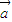
•
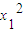
+
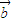
•x
1+
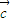
=0,
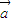
•
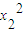
+
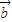
•x
2+
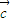
=0.把这两个等式相减可得 (x
1-x
2)[(x
1+x
2)
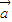
+
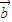
]=0.由于(x
1+x
2)
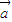
+
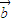
≠0,可得 x
1-x
2=0.
解答:解:由于关于x的方程
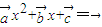
的两个根为x
1,x
2,故有
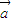
•
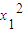
+
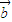
•x
1+
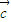
=0,
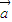
•
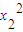
+
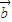
•x
2+
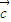
=0.
把这两个等式相减可得 (x
1-x
2)[(x
1+x
2)
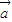
+
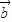
]=0.
由于
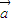
、
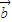
、
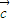
是三个非零向量,且
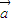
、
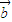
不共线,∴(x
1+x
2)
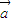
+
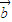
≠0,∴x
1-x
2=0,
故选B.
点评:本题主要考查两个向量共线的条件,得到(x
1-x
2)[(x
1+x
2)
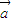
+
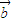
]=0,是解题的关键,属于中档题.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
设
,,是三个非零向量,给出以下四个命题:
①若
•+||||=0,则
∥
;
②若
2=2,则
=或
=-;
③若
|+|=|-|,则
⊥;
④若
•=•,则
=.
则所有正确命题的序号为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
设命题p:{
,
,
}为空间的一个基底,命题q:
、
、
是三个非零向量,则命题p是q的
充分不必要
充分不必要
条件.
查看答案和解析>>
科目:高中数学
来源:
题型:
设命题p:
,,是三个非零向量;命题q:
{,,}为空间的一组基,则命题q是命题p的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学
来源:
题型:
(2012•绍兴一模)设
、
、
是三个非零向量,且
、
不共线,若关于x的方程
x2+x+=的两个根为x
1,x
2,则( )
查看答案和解析>>

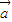 、
、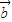 、
、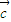 是三个非零向量,且
是三个非零向量,且 、
、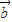 不共线,若关于x的方程
不共线,若关于x的方程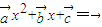 的两个根为x1,x2,则( )
的两个根为x1,x2,则( ) 步步高达标卷系列答案
步步高达标卷系列答案