
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() .过
.过![]() 作一个平面
作一个平面![]() 使得
使得![]() 平面
平面![]() .
.
(1)求平面![]() 将四棱锥
将四棱锥![]() 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;
(2)若平面![]() 与平面
与平面![]() 之间的距离为
之间的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)![]() 或
或![]() .(2)
.(2)![]()
【解析】试题分析:(1)设平面![]() 与直线
与直线![]() 分别交于
分别交于![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,可得
,可得![]() 分别是
分别是![]() 的中点,根据棱锥的体积公式可得
的中点,根据棱锥的体积公式可得![]() ,从而可得平面
,从而可得平面![]() 将四棱锥
将四棱锥![]() 分成两部分几何体的体积之比;(2)因为
分成两部分几何体的体积之比;(2)因为![]() 两两垂直,以
两两垂直,以![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,分别求出直线
轴建立空间直角坐标系,分别求出直线![]() 的方向向量以及平面
的方向向量以及平面![]() 的一个法向量,利用空间向量夹角余弦公式可得直线
的一个法向量,利用空间向量夹角余弦公式可得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)记平面![]() 与直线
与直线![]() .
.
因为![]() ,所以
,所以![]() .
.
由已知条件易知![]() ,又因
,又因![]() .
.
所以![]()
可得![]()
所以![]() .
.
即平面![]() 将四棱锥
将四棱锥![]() 分成两部分几何体的体积之比为
分成两部分几何体的体积之比为![]() .
.
(2)建立直角坐标系,记![]()
则![]()
因为平面![]() 的法向量
的法向量![]()
![]()
设![]()
![]() 得
得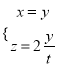 ,
,
取![]() 得平面
得平面![]() .
.
由条件易知点![]() 到平面
到平面![]() 距离
距离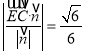 .即
.即![]() .
.
所以![]() .直线
.直线![]() 与平面
与平面![]() 所成角
所成角![]() 满足
满足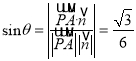
【方法点晴】本题主要考查棱锥的体积公式以及利用空间向量线面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
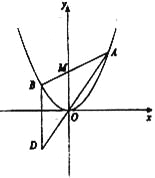
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G:x2=2py(p>0),直线y=k(x﹣1)+2与抛物线G相交A(x1 , y1),B(x2 , y2)(x1<x2),过A,B点分别作抛物线G的切线L1 , L2 , 两切线L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求抛物线G的方程;
(2)若p=2,△ABH的面积为S1 , 直线AB与抛物线G围成封闭图形的面积为S2 , 证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从参加环保知识竟赛的学生中抽取了部分学生的成绩进行分析,不过作好的茎叶图和频率分布直方图因故均受到不同程度的损坏,其可见部分信息如图所示,据此解答下列问题:

(1)求抽取学生成绩的中位数,并修复频率分布直方图;
(2)根据修复的频率分布直方图估计该中学此次环保知识竞赛的平均成绩。(以各组的区间中点值代表该组的各个值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,正确命题的个数是( )
①命题“若x=y,则sinx=siny”的逆否命题是真命题;
②已知α,β是不同的平面,m,n是不同的直线,m∥α,n∥β,α⊥β,则m⊥n;
③直线l1:2ax+y+1=0,l2:x+2ay+2=0,l1∥l2的充要条件是 ![]() ;
;
④ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
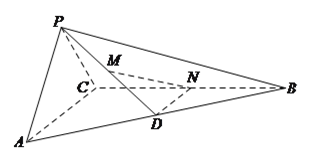
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上.
上.
(![]() )当
)当![]() 为
为![]() 的中点时,证明:
的中点时,证明: ![]() 平面
平面![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )是否存在点
)是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明天小强要参加班里组织的郊游活动,为了做好参加这次郊游的准备工作,他测算了如下数据:整理床铺、收拾携带物品8分钟,洗脸、刷牙7分钟,煮牛奶15分钟,吃早饭10分钟,查公交线路图9分钟,给出差在外的父亲发手机短信6分钟,走到公共汽车站10分钟,等公共汽车10分钟.小强粗略地算了一下,总共需要75分钟,为了赶上7:50的公共汽车,小强决定6:30起床,不幸的是他一下子睡到6:50,请你帮小强安排一下时间,画出一份郊游出行前时间安排流程图,使他还能来得及参加此次郊游.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com