
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).![]() 是曲线
是曲线![]() 上的动点,将线段
上的动点,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(I)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(II)在(I)的条件下,若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点(除极点外),且有定点
两点(除极点外),且有定点![]() ,求
,求![]() 面积.
面积.
科目:高中数学 来源: 题型:
【题目】如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )

A.120种B.240种C.144种D.288种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身倡导全民做到每天参加一次以上的体育健身活动,旨在全面提高国民体质和健康水平.某市的体育部门对某小区的4000人进行了“运动参与度”统计评分(满分100分),得到了如下的频率分布直方图:
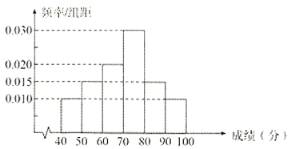
(1)求这4000人的“运动参与度”的平均得分![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为这4000人的“运动参与度”的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别取平均得分
分别取平均得分![]() 和方差
和方差![]() ,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
,那么选取的4000人中“运动参与度”得分超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用这4000人得分的情况来估计全市所有人的得分情况,现从全市随机抽取4人,记“运动参与度”的得分不超过84.81分的人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班教室桌椅6排7列,有40名同学.空出最后一排的某两个位置,其余人按身高和视力排座位.班中有24人身高高,有18人视力好,其中,有6名同学同时具备此两个条件.已知若一名同学个子矮视力又不好,则他必须坐在前三排;若一名同学个子高视力又好,则他必须坐在最后三排.设排座位的方法是![]() ,则
,则![]() 的质因数分解中的2的次数是______.
的质因数分解中的2的次数是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全力抗击“新冠疫情”对全球做出了巨大贡献,广大中小学生在这场“战疫”中也通过各种方式作出了贡献.某校团委准备组织一次“网上战疫”的宣传活动,活动包含4项子活动.现随机抽取了5个班级中的25名同学进行关于活动方案的问卷调查,其中关于4项子活动的赞同情况统计如下:
班级代码 | A | B | C | D | E | 合计 |
4项子活动全部赞同的人数 | 3 | 4 | 8 | 3 | 2 | 20 |
4项子活动不全部赞同的人数 | 1 | 1 | 0 | 2 | 1 | 5 |
合计问卷调查人数 | 4 | 5 | 8 | 5 | 3 | 25 |
现欲针对4项子活动的活动内容作进一步采访调研,每项子活动采访1名学生.
(1)若每项子活动都从这25名同学中随机选取1人采访,求4次采访中恰有1次采访的学生对“4项子活动不全部赞同”的概率;
(2)若从A班和E班的被问卷调查者中各随机选取2人作为采访调研的对象,记选取的4人中“4项子活动全部赞同”的人数为X,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有编号依次为1,2,3,4,5,6的6名学生参加数学竞赛选拔,今有甲,乙,丙,丁四位老师在猜谁将获得第一名,甲猜不是3号就是5号;乙猜6号不可能;丙猜是1号,2号,4号中的一个;丁猜2号,3号,4号都不可能,若以上四位老师只有一位猜对,则猜对者是___________(填甲、乙、丙、丁)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com