
分析 由条件利用正弦函数的图象特征,正弦函数的图象的对称性、单调性,函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 ???解:对于f(x)=sin(2x-$\frac{π}{3}$),
令x=$\frac{11π}{12}$,求得f(x)=-1,为函数的最小值,故它的图象C关于直线x=$\frac{11π}{12}$对称故①正确.
令x=$\frac{2π}{3}$,求得f(x)=0,可得它的图象C关于点($\frac{2π}{3}$,0)对称,故②正确.
令-$\frac{π}{12}$≤x≤$\frac{5π}{2}$,可得-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤$\frac{14π}{3}$,故函数f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{2}$)内不存在单调性,故排除③,
由y=sin2x的图象向右平移$\frac{π}{3}$个单位长度可以得到y=sin2(x-$\frac{π}{3}$)=sin(2x-$\frac{2π}{3}$),故排除④,
故答案为:①②.
点评 本题主要考查正弦函数的图象特征,正弦函数的图象的对称性、单调性,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|α=475°+k•360°,k∈Z} | B. | α|α=97°+k•360°,k∈Z} | ||
| C. | α|α=263°+k•360°,k∈Z} | D. | α|α=-263°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
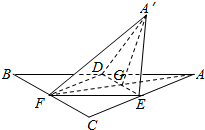 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有DE⊥平面A′GF | |
| C. | 三棱锥A′-FED的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com