练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】编号分别为的12名篮球运动员在某次篮球比赛中的得分记录如下：

    运动员编号

    得分

    5

    10

    12

    16

    8

    21

    27

    15

    6

    22

    18

    29

    （1）完成如下的频率分布表：

    得分区间

    频数

    频率

    3

    合计

    （2）从得分在区间内的运动员中随机抽取2人，求这2人得分之和大于25的概率.

    【答案】（1）分布表见解析；（2）0.8.

    【解析】

    （1）根据频数、频率的定义即可得到答案.

    （2）首先利用列举法写出从内的运动员中随机抽取2人的全部基本事件，计算2人得分之和大于25的基本事件个数，再利用古典概型公式计算即可.

    （1）频率分布表：

    得分区间

    频数

    频率

    3

    5

    4

    合计

    12

    （2）得分在区间的运动员编号为：，从中随机抽取2人，

    所以的可能抽取结果：，

    共10种，

    设得分在区间内的运动员中随机抽取2人，求这 2人得分之和大于25的概率记为时间，事件包含个基本事件，

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某校高一、高二、高三的学生志愿者人数分别为180，180，90．现采用分层抽样的方法从中抽取5名学生去某敬老院参加献爱心活动，若再从这5人中抽取2人作为负责人，则事件“抽取的2名同学来自不同年级”的概率是( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为计算， 设计了如图所示的程序框图，则空白框中应填入（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆（）的离心率为，且经过点.

    （1）求椭圆的方程；

    （2）过点作直线与椭圆交于不同的两点，，试问在轴上是否存在定点使得直线与直线恰关于轴对称？若存在，求出点的坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次数学竞赛中，某些选手是朋友关系.记所有选手的集合为X，对集合X的子集Y，若可以将这些人两两分组，且每组中两名选手均是朋友关系，则称子集Y“可两两分组”.已知集合X不可两两分组，且对于任意选手，若A、B不是朋友关系，则可两两分组，且X中没有一个人与其他所有人均为朋友关系证明:对任意选手，若a、b为朋友关系，b、c为朋友关系，则a、c也为朋友关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表.

    月收入(单位百元)

    频数

    5

    10

    15

    10

    5

    5

    赞成人数

    4

    8

    12

    5

    2

    1

    (1)由以上统计数据填下面2×2列联表，并问是否有99％的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异；

    月收入不低于55百元的人数

    月收入低于55百元的人数

    合计

    赞成

    a=______________

    c=______________

    ______________

    不赞成

    b=______________

    d=______________

    ______________

    合计

    ______________

    ______________

    ______________

    (2)试求从年收入位于（单位：百元）的区间段的被调查者中随机抽取2人，恰有1位是赞成者的概率。

    参考公式：，其中.

    参考值表：

    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用n种不同的颜色为下列两块广告牌着色，（如图甲、乙），要求在A，B，C，D四个区域中相邻（有公共边界）的区域不用同一颜色.

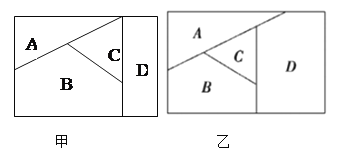
    （1）若n=6,则为甲图着色时共有多少种不同的方法；

    （2）若为乙图着色时共有120种不同方法，求n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l的参数方程为(t为参数)，它与曲线C：(y－2)2－x2＝1交于A、B两点．

    (1)求|AB|的长；

    (2)以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为，求点P到线段AB中点M的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

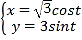    【题目】在平面直角坐标系xOy中，曲线的参数方程为（t为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是，曲线的极坐标方程是．

    （1）求直线l和曲线的直角坐标方程，曲线的普通方程；

    （2）若直线l与曲线和曲线在第一象限的交点分别为P，Q，求的值．

    查看答案和解析>>

    同步练习册答案