
分析 (1)运用3级等比数列的概念,结合三角函数的化简,即可得到所求;
(2)由新定义,可得{an}为2级等比数列,即有$\frac{{a}_{n}+2}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-2}}$,则{a2n-1},{a2n}均成等比数列,
设等比数列{a2n-1},{a2n}的公比分别为q1,q2(q1q2≠0),{an}为3级等比数列,即有$\frac{{a}_{n}+3}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-3}}$,
则{a3n-2}成等比数列,设公比为Q(Q≠0).再由a1,a7;a4,a10为等比数列中的项,运用等比数列的通项公式可得q1,q2相等,再由等比数列的定义,即可得证.
解答 解:(1){an}是3级等比数列,即有$\frac{{a}_{n}+3}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-3}}$,
[2nsin(ωn+$\frac{π}{6}$)]2=2n-3sin[(ωn+$\frac{π}{6}$)-3ω]2n+3sin[(ωn+$\frac{π}{6}$)+3ω],
sin2(ωn+$\frac{π}{6}$)=sin[(ωn+$\frac{π}{6}$)-3ω]sin[(ωn+$\frac{π}{6}$)+3ω]
=sin2(ωn+$\frac{π}{6}$)cos23ω-cos2(ωn+$\frac{π}{6}$)sin23ω
=sin2(ωn+$\frac{π}{6}$)(1-sin23ω)-[1-sin2(ωn+$\frac{π}{6}$)]sin23ω
=sin2(ωn+$\frac{π}{6}$)-sin23ω,
∴sin23ω=0,3ω=kπ(k∈Z),∴ω=$\frac{kπ}{3}$ (k∈Z),
∴ω∈{ω|ω=$\frac{kπ}{3}$,k∈Z}.
(2)若{an}为2级等比数列,$\frac{{a}_{n}+2}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-2}}$,
则{a2n-1},{a2n}均成等比数列,
设等比数列{a2n-1},{a2n}的公比分别为q1,q2(q1q2≠0),
{an}为3级等比数列,$\frac{{a}_{n}+3}{{a}_{n}}$=$\frac{{a}_{n}}{{a}_{n-3}}$,
则{a3n-2}成等比数列,设公比为Q(Q≠0).
a1,a7既是{a2n-1}中的项,也是{a3n-2}中的项,$\frac{{a}_{7}}{{a}_{1}}$=q13=Q2,
a4,a10既是{a2n}中的项,也是{a3n-2}中的项,$\frac{{a}_{10}}{{a}_{4}}$=q23=Q2,
${q}_{1}^{3}$=${q}_{2}^{3}$=Q2,∴q1=q2.
设q1=q2=q2(q≠0),则Q=q3,
所以a2n-1=a1qn-1=a1q2n-2(n∈N*),
a2n=a2q2n-1=a2q2n-2(n∈N*),
又a4=a1Q=a1q3,a4=a2q2=a2q2,
所以a2=a1q,
a2n=a1q2n-1(n∈N*),
所以,a2n-1=a1q2n-2,a2n=a1q2n-1(n∈N*),
综合得:an=a1qn-1(n∈N*),显然{an}为等比数列.
点评 本题考查新定义的理解和运用,考查三角函数的化简,同时考查等比数列的通项公式和性质,以及推理能力,有一定的难度.


科目:高中数学 来源: 题型:解答题
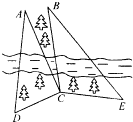 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com