对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),则称f(x)为“局部奇函数”.
(Ⅰ)已知二次函数f(x)=ax2+2x-4a(a∈R),试判断f(x)是否为“局部奇函数”?并说明理由;
(Ⅱ)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围;
(Ⅲ)若f(x)=4x-m2x+1+m2-3为定义域R上的“局部奇函数”,求实数m的取值范围.
解:f(x)为“局部奇函数”等价于关于x的方程f(-x)=-f(x)有解.
(Ⅰ)当f(x)=ax
2+2x-4a(a∈R),时,
方程f(-x)=-f(x)即2a(x
2-4)=0,有解x=±2,
所以f(x)为“局部奇函数”. …
(Ⅱ)当f(x)=2
x+m时,f(-x)=-f(x)可化为2
x+2
-x+2m=0,
因为f(x)的定义域为[-1,1],所以方程2
x+2
-x+2m=0在[-1,1]上有解.…
令
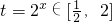
,则
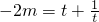
.
设

,则

,
当t∈(0,1)时,g'(t)<0,故g(t)在(0,1)上为减函数,
当t∈(1,+∞)时,g'(t)>0,故g(t)在(1,+∞)上为增函数. …
所以t∈[
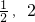
]时,g(t)
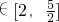
.
所以

,即

. …
(Ⅲ)当f(x)=4
x-m2
x+1+m
2-3时,f(-x)=-f(x)可化为4
x+4
-x-2m(2
x+2
-x)+2m
2-6=0.
t=2
x+2
-x≥2,则4
x+4
-x=t
2-2,
从而t
2-2mt+2m
2-8=0在[2,+∞)有解即可保证f(x)为“局部奇函数”.…
令F(t)=t
2-2mt+2m
2-8,
1° 当F(2)≤0,t
2-2mt+2m
2-8=0在[2,+∞)有解,
由当F(2)≤0,即2m
2-4m-4≤0,解得1-
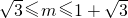
; …
2° 当当F(2)>0时,t
2-2mt+2m
2-8=0在[2,+∞)有解等价于

解得

. …
(说明:也可转化为大根大于等于2求解)
综上,所求实数m的取值范围为
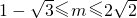
. …
分析:利用局部奇函数的定义,建立方程关系,然后判断方程是否有解即可.
点评:本题主要考查新定义的应用,利用新定义,建立方程关系,然后利用函数性质进行求解是解决本题的关键,考查学生的运算能力.

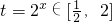 ,则
,则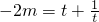 .
. ,则
,则 ,
,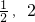 ]时,g(t)
]时,g(t)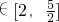 .
. ,即
,即 . …
. …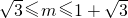 ; …
; … 解得
解得 . …
. …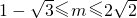 . …
. …

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案