
分析 M,G,N三点共线,存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AM}$+(1-m)$\overrightarrow{AN}$=mx$\overrightarrow{AB}$+(1-m)y$\overrightarrow{AC}$,又G是△ABC的重心,可得$\overrightarrow{AG}$=$\frac{1}{3}$$(\overrightarrow{AB}+\overrightarrow{AC})$,结合基本不等式的性质即可得出.
解答 解:∵M,G,N三点共线,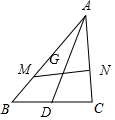
∴存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AM}$+(1-m)$\overrightarrow{AN}$=mx$\overrightarrow{AB}$+(1-m)y$\overrightarrow{AC}$,
又∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$$(\overrightarrow{AB}+\overrightarrow{AC})$=mx$\overrightarrow{AB}$+(1-m)y$\overrightarrow{AC}$,
∴mx=$\frac{1}{3}$,(1-m)y=$\frac{1}{3}$,
∴$\frac{1}{3x}+\frac{1}{3y}$=1,即$\frac{1}{x}+\frac{1}{y}$=3.
∴x+y=(x+y)$•\frac{1}{3}(\frac{1}{x}+\frac{1}{y})$=$\frac{1}{3}(2+\frac{y}{x}+\frac{x}{y})$≥$\frac{1}{3}(2+2\sqrt{\frac{x}{y}•\frac{y}{x}})$=$\frac{4}{3}$,当且仅当x=y=$\frac{2}{3}$时取等号.
故答案为:$\frac{4}{3}$.
点评 本题考查了、向量共线对立、三角形重心性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,BC⊥平面AA1C1C,BC=CA=AA1=2,∠CAA1=60°.
如图,三棱柱ABC-A1B1C1中,BC⊥平面AA1C1C,BC=CA=AA1=2,∠CAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com