
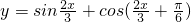 的图象中相邻两对称轴的距离是 ________.
的图象中相邻两对称轴的距离是 ________.科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 19 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| x+3 |
| x-1 |
查看答案和解析>>
科目:高中数学 来源:四川省成都石室中学2012届高三上学期期中考试数学文科试题 题型:022
给出以下五个命题:
①y=cos(x-![]() )cos(x+
)cos(x+![]() )的图象中相邻两个对称中心的距离为π;
)的图象中相邻两个对称中心的距离为π;
②y=![]() 的图象关于点(-1,1)对称;
的图象关于点(-1,1)对称;
③关于X的方程ax2-2ax-1=0有且仅有一个实根,则a=-1
④命题P:对任意x∈R,都有sinx≤1;则![]() p存在x∈R,使得sinx>1;
p存在x∈R,使得sinx>1;
⑤函数y=3x+3-x(x<0)的最小值为2.其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市麻城实验高中高三(上)12月月考数学试卷(解析版) 题型:解答题
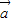 =(sinωx,-cosωx),
=(sinωx,-cosωx),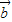 =(
=(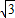 cosωx,cosωx)(ω>0),函数f(x)=
cosωx,cosωx)(ω>0),函数f(x)= .
.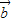 +
+ ,且函数f(x)=
,且函数f(x)=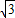 sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+ 的图象中任意两相邻对称轴间的距离为π.
的图象中任意两相邻对称轴间的距离为π. ,且c=2
,且c=2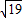 ,△ABC的面积S=2
,△ABC的面积S=2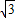 ,求a+b的值.
,求a+b的值.查看答案和解析>>
科目:高中数学 来源:四川省期中题 题型:填空题
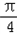 )cos(x+
)cos(x+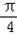 )的图象中相邻两个对称中心的距离为π;
)的图象中相邻两个对称中心的距离为π;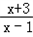 的图象关于点(﹣1,1)对称;
的图象关于点(﹣1,1)对称;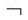 p:存在x∈R,使得sinx>1;
p:存在x∈R,使得sinx>1;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com