
专家由圆x +y
+y =a
=a 的面积S=
的面积S= a
a 通过类比推理猜想椭圆
通过类比推理猜想椭圆 的面积S=
的面积S= ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|
ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|  }, 点集B="{(x," y)|
}, 点集B="{(x," y)| 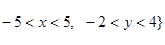 , 则点集M="{(x," y)|x=x
, 则点集M="{(x," y)|x=x +x
+x , y=y
, y=y +y
+y , (x
, (x , y
, y )
) A, (x
A, (x , y
, y )
) B}所表示的区域的面积为_____________.
B}所表示的区域的面积为_____________.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:填空题
我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-3,4),且法向量为 =(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为
=(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为 =(-1,-2,1)的平面的方程为____________ .
=(-1,-2,1)的平面的方程为____________ .
(化简后用关于x,y,z的一般式方程表示)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察下列等式:
12=1,
12—22=—3,
12—22+32=6,
12—22+32—42=-10,
…………………
由以上等式推测到一个一般的结论:对于 ,12—22+32—42+…+(—1)n+1n2=
,12—22+32—42+…+(—1)n+1n2=
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
边长为 的等边三角形内任一点到三边距离之和为定值,则这个定值为
的等边三角形内任一点到三边距离之和为定值,则这个定值为 ;
;
推 广到空间,棱长为
广到空间,棱长为 的正四面体内任一点到各面距离之和为___________________.
的正四面体内任一点到各面距离之和为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com