
【题目】已知函数![]() .
.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)当![]() 时,在区间
时,在区间![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)m=2,n=﹣1;(2)![]() .
.
【解析】分析:(1)求出函数的导数,结合切点坐标求出![]() ,
,![]() 的值即可;
的值即可;
(2)求出函数的导数,通过讨论m的范围,求出函数的单调区间,从而求出m的范围即可.
详解:(1)∵f′(x)=﹣![]() +n,
+n,
故f′(0)=n﹣m,即n﹣m=﹣3,
又∵f(0)=m,故切点坐标是(0,m),
∵切点在直线y=﹣3x+2上,
故m=2,n=﹣1;
(2)∵f(x)=![]() +x,∴f′(x)=
+x,∴f′(x)=![]() ,
,
当m≤0时,f′(x)>0,
故函数f(x)在(﹣∞,1)递增,
令x0=a<0,此时f(x)<0,符合题意,
当m>0时,即0<m<e时,则函数f(x)在(﹣∞,lnm)递减,在(lnm,+∞)递增,
①当lnm<1即0<m<e时,则函数f(x)在(﹣∞,lnm)递减,在(lnm,1]递增,
f(x)min=f(lnm)=lnm+1<0,解得:0<m<![]() ,
,
②当lnm>1即m≥e时,函数f(x)在区间(﹣∞,1)递减,
则函数f(x)在区间(﹣∞,1)上的最小值是f(1)=![]() +1<0,解得:m<﹣e,无解,
+1<0,解得:m<﹣e,无解,
综上,m<![]() ,即m的范围是(﹣∞,
,即m的范围是(﹣∞,![]() ).
).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=an+n,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是( ) 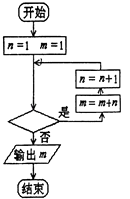
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某居民小区有两个相互独立的安全防范系统(简称系统)![]() 和
和![]() ,系统
,系统![]() 和
和![]() 在任意时刻发生故障的概率分别为
在任意时刻发生故障的概率分别为![]() 和
和![]() 。
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)设系统![]() 在3次相互独立的检测中不发生故障的次数为随机变量
在3次相互独立的检测中不发生故障的次数为随机变量![]() ,求
,求![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,作为国家战略性空间基础设施,我国北斗卫星导航系统不仅对国防安全意义重大,而且在民用领域的精准化应用也越来越广泛.据统计,2016年卫星导航与位置服务产业总产值达到2118亿元,较2015年约增长![]() .下面是40个城市北斗卫星导航系统与位置服务产业的产值(单位:万元)的频率分布直方图:
.下面是40个城市北斗卫星导航系统与位置服务产业的产值(单位:万元)的频率分布直方图:
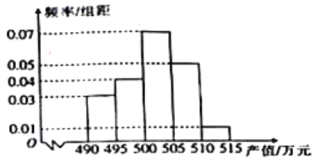
(1)根据频率分布直方图,求产值小于500万元的城市个数;
(2)在上述抽取的40个城市中任取2个,设![]() 为产值不超过500万元的城市个数,求
为产值不超过500万元的城市个数,求![]() 的分布列及期望和方差.
的分布列及期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(1)规定每日底薪50元,快递业务每完成一单提成3元;方案(2)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图。
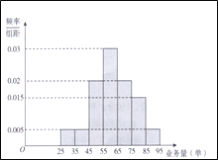
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案(1),丙、丁选择了日工资方案(2).现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案(1)的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明某型号汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数为
(千米/小时)的函数为![]()
![]() .
.
(1)当![]() 千米/小时时,行驶
千米/小时时,行驶![]() 千米耗油量多少升?
千米耗油量多少升?
(2)若油箱有![]() 升油,则该型号汽车最多行驶多少千米?
升油,则该型号汽车最多行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com